题目内容
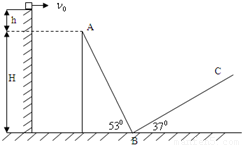
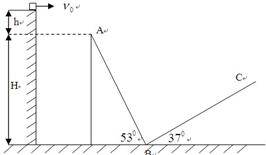
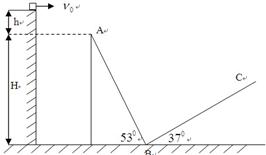
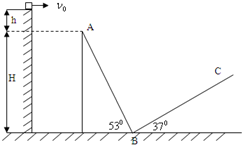 如图所示,一物块质量m=1.0kg自平台上以速度ν0水平抛出,刚好落在邻近一倾角为α=53°的粗糙斜面AB顶端,并恰好沿该斜面下滑,已知斜面顶端与平台的高度差h=0.032m,粗糙斜面BC倾角为β=37°,足够长.物块与两斜面间的动摩擦因数均为μ=0.5,A点离B点所在平面的高度H=1.2m.物块在斜面上运动的过程中始终未脱离斜面,不计在B点的机械能损失.最大静摩擦力等于滑动摩擦力,cos37°=0.8,sin37°=0.6.(g取10m/s2)
如图所示,一物块质量m=1.0kg自平台上以速度ν0水平抛出,刚好落在邻近一倾角为α=53°的粗糙斜面AB顶端,并恰好沿该斜面下滑,已知斜面顶端与平台的高度差h=0.032m,粗糙斜面BC倾角为β=37°,足够长.物块与两斜面间的动摩擦因数均为μ=0.5,A点离B点所在平面的高度H=1.2m.物块在斜面上运动的过程中始终未脱离斜面,不计在B点的机械能损失.最大静摩擦力等于滑动摩擦力,cos37°=0.8,sin37°=0.6.(g取10m/s2)(1)物块水平抛出的初速度ν0是多少.
(2)若取A所在水平面为零势能面,求物块第一次到达B点的机械能.
(3)从滑块第一次到达B点时起,经0.6s正好通过C点,求BC之间的距离.
分析:(1)小球水平抛出后刚好能沿光滑斜面下滑,说明此时小球的速度的方向恰好沿着斜面的方向,由速度分析可以求得初速度的大小;
(2)从A到B的运动过程中,由动能定理求出物块第一次到达B点的速度大小,即可求出第一次到达B点的机械能.
(3)滑块沿BC段先向上做匀减速运动,后向下做匀加速运动,根据牛顿第二定律求出加速度,由运动学公式求解BC距离.
(2)从A到B的运动过程中,由动能定理求出物块第一次到达B点的速度大小,即可求出第一次到达B点的机械能.
(3)滑块沿BC段先向上做匀减速运动,后向下做匀加速运动,根据牛顿第二定律求出加速度,由运动学公式求解BC距离.
解答:解:(1).物块自平台做平抛运动,由平抛运动知识得:
νy=
=
=0.8m/s
由于物块恰好沿斜面下滑,则:νA=
=
m/s=1m/s
ν0=νAcos530=0.6m/s
(2).物块在A点时的速度:νA=1m/s.
从A到B的运动过程中,由动能定理得:
mgH-μmgcos530
=
mvB2-
mvA2
解得,物块在B点时的速度:vB=4m/s
故在B点时的机械能:EB=
mvB2-mgH=-4J
(3).滑块沿BC段向上运动时的加速度大小:
a1=g(sin370+μcos370)=10m/s2
运动的时间为t1=
=0.4s,则物块下滑时间为:t=0.2s.
返回时的加速度大小:a2=g(sin370-μcos370)=2m/s2
BC间的距离:XBC=
-
a2(t-
)2=0.76m
答:(1)物块水平抛出的初速度ν0是0.6m/s.
(2)若取A所在水平面为零势能面,物块第一次到达B点的机械能是-4J.
(3)从滑块第一次到达B点时起,经0.6s正好通过C点,BC之间的距离是0.76m.
νy=
| 2gh |
| 2×10×0.032 |
由于物块恰好沿斜面下滑,则:νA=
| νy |
| sin530 |
| 0.8 |
| 0.8 |
ν0=νAcos530=0.6m/s
(2).物块在A点时的速度:νA=1m/s.
从A到B的运动过程中,由动能定理得:
mgH-μmgcos530
| H |
| sin530 |
| 1 |
| 2 |
| 1 |
| 2 |
解得,物块在B点时的速度:vB=4m/s
故在B点时的机械能:EB=
| 1 |
| 2 |
(3).滑块沿BC段向上运动时的加速度大小:
a1=g(sin370+μcos370)=10m/s2
运动的时间为t1=
| vB |
| a1 |
返回时的加速度大小:a2=g(sin370-μcos370)=2m/s2
BC间的距离:XBC=
| vB2 |
| 2a1 |
| 1 |
| 2 |
| vB |
| a1 |
答:(1)物块水平抛出的初速度ν0是0.6m/s.
(2)若取A所在水平面为零势能面,物块第一次到达B点的机械能是-4J.
(3)从滑块第一次到达B点时起,经0.6s正好通过C点,BC之间的距离是0.76m.
点评:小球在接触斜面之前做的是平抛运动,在斜面上时小球做匀加速直线运动,根据两个不同的运动的过程,分段求解即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
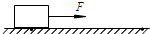 如图所示,一物块质量m=2kg,在与水平拉力F=8N的作用下,沿水平面由静止向右运动一段距离x=5m,若物块与地面间的动摩擦因数μ=0.2,重力加速度g取10m/s2.求:
如图所示,一物块质量m=2kg,在与水平拉力F=8N的作用下,沿水平面由静止向右运动一段距离x=5m,若物块与地面间的动摩擦因数μ=0.2,重力加速度g取10m/s2.求: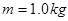 自平台上以速度
自平台上以速度 水平抛出,刚好落在邻近一倾角为
水平抛出,刚好落在邻近一倾角为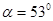 的粗糙斜面
的粗糙斜面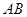 顶端,并恰好沿该斜面下滑,已知斜面顶端与平台的高度差
顶端,并恰好沿该斜面下滑,已知斜面顶端与平台的高度差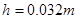 ,粗糙斜面
,粗糙斜面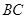 倾角为
倾角为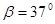 ,足够长。物块与两斜面间的动摩擦因数均为
,足够长。物块与两斜面间的动摩擦因数均为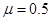 ,
, 点离
点离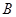 点所在平面的高度
点所在平面的高度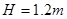 。物块在斜面上运动的过程中始终未脱离斜面,不计在
。物块在斜面上运动的过程中始终未脱离斜面,不计在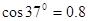 ,
,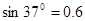 。(
。( 取
取 )
)
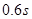 正好通过
正好通过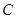 点,求
点,求 自平台上以速度
自平台上以速度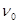 水平抛出,刚好落在邻近一倾角为
水平抛出,刚好落在邻近一倾角为 的粗糙斜面
的粗糙斜面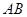 顶端,并恰好沿该斜面下滑,已知斜面顶端与平台的高度差
顶端,并恰好沿该斜面下滑,已知斜面顶端与平台的高度差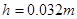 ,粗糙斜面
,粗糙斜面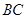 倾角为
倾角为 ,足够长。物块与两斜面间的动摩擦因数均为
,足够长。物块与两斜面间的动摩擦因数均为 ,
,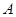 点离
点离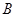 点所在平面的高度
点所在平面的高度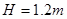 。物块在斜面上运动的过程中始终未脱离斜面,不计在
。物块在斜面上运动的过程中始终未脱离斜面,不计在 ,
,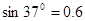 。(
。(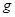 取
取 )
)
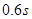 正好通过
正好通过 点,求
点,求