题目内容
质量为m的木块以水平初速度V0在水平地面上最多能滑行的距离为S,现在其上面固定一块同样的木块,使它们一起以2V0的初速度在同一水平地面上滑行,则最多能滑行的距离是( )
分析:根据牛顿第二定律求出物体与水平面间的动摩擦因数,结合牛顿第二定律和运动学公式求出速度为2v0时滑行的距离.
解答:解:物体滑动的加速度a=
,又a=
=
=μg
上面固定一块同样的木块,加速度a′=
=
=μg=
则滑行的距离s′=
=4s.
故选D
| v02 |
| 2s |
| F |
| m |
| μmg |
| m |
上面固定一块同样的木块,加速度a′=
| F |
| m |
| μ2mg |
| 2m |
| v02 |
| 2s |
则滑行的距离s′=
| 4v02 |
| 2a′ |
故选D
点评:本题综合考查了牛顿第二定律和运动学公式,难度不大,知道加速度是联系力学和运动学的桥梁.

练习册系列答案
相关题目
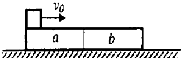 如图所示,在光滑水平面上静止地放着质量为2m的木板,一质量为m的木块以水平初速v0在木板上由左端恰能滑至木板的右端与木板相对静止.现将木板分成长度与质量相等的a、b两段后紧挨着仍静置于光滑水平面上,让木块仍以相同的初速度v0由木板a上的左端开始滑动,若木块运动过程中所受摩擦力始终保持不变,则( )
如图所示,在光滑水平面上静止地放着质量为2m的木板,一质量为m的木块以水平初速v0在木板上由左端恰能滑至木板的右端与木板相对静止.现将木板分成长度与质量相等的a、b两段后紧挨着仍静置于光滑水平面上,让木块仍以相同的初速度v0由木板a上的左端开始滑动,若木块运动过程中所受摩擦力始终保持不变,则( )| A、木块滑到木板b的右端后飞离木板 | B、木块仍能滑到木板b的右端并与木板保持相对静止 | C、木块滑到木板b的右端前就与木板保持相对静止 | D、后一过程产生的热量小于原来过程产生的热量 |
 如图所示质量为M的长木板静止在光滑平面上,另一质量为m的木块以水平初速度v0从左端滑上长木板,经时间t从长木板的另一端滑下.若木块和长木板之间的动摩擦因数为μ,求木块滑下时长木板的速度.
如图所示质量为M的长木板静止在光滑平面上,另一质量为m的木块以水平初速度v0从左端滑上长木板,经时间t从长木板的另一端滑下.若木块和长木板之间的动摩擦因数为μ,求木块滑下时长木板的速度.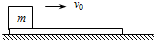 如图所示,将一质量为3m的长木板静止地放在水平面上,另一质量为m的木块以水平初速度v0滑上长木板,若木块与木板、木板与桌面间的动摩擦因数均为μ,则在木块与长木板相对静止之前,长木板受桌面的摩擦力大小为( )
如图所示,将一质量为3m的长木板静止地放在水平面上,另一质量为m的木块以水平初速度v0滑上长木板,若木块与木板、木板与桌面间的动摩擦因数均为μ,则在木块与长木板相对静止之前,长木板受桌面的摩擦力大小为( )