Question

【题目】在桌面上有一个倒立的玻璃圆锥，其顶点恰好与桌面接触，圆锥的轴（图中虚线）与桌面垂直，过轴线的截面为等边三角形，如图所示．有一半径为r=0.1m的圆柱形平行光束垂直入射到圆锥面上，光束的中心轴与圆锥的轴重合．已知光在真空中传播速度c=3.0×l08m/s，玻璃的折射率为n= ．则：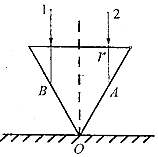

（Ⅰ）通过计算说明光线1能不能在圆锥的侧面B点发生全反射？
（Ⅱ）光线1经过圆锥侧面B点后射到桌面上某一点所用的总时间是多少？（结果保留三位有效数字）

Answer 1

【答案】解：（I）设全反射临界角为C，由sinC=
得 C=arcsin ＜60°；
由几何知识可得，光线1射到圆锥侧面上时的入射角为 i=60°
所以 i＞C
所以，光线1能在圆锥的侧面B点发生全反射．
（Ⅱ）根据几何关系知 BE=EF=2rsin60°= r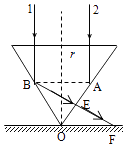

光在玻璃中的速度 v=
所以，总时间 t= +
代入数据解得 t≈1.58×10﹣9s
答：（I）光线1能在圆锥的侧面B点发生全反射．
（Ⅱ）光线1经过圆锥侧面B点后射到桌面上某一点所用的总时间是1.58×10﹣9s．
【解析】（I）当半径为r的圆柱形平行光束垂直入射到圆锥的地面上，经过第一次折射时，由于入射角等于零，所以折射角也是零，因此折射光线不发生偏折．当第二次折射时，由于入射角等于60°，而玻璃的折射率为1.73，可得入射角与临界角的大小，所以会发生光的全反射，反射光线却恰好垂直射出．（Ⅱ）可根据几何关系可确定光线在圆锥内和外通过的路程，由v= 求出光线在玻璃中的速度，由运动学公式即可求解时间．
【考点精析】解答此题的关键在于理解光的折射的相关知识，掌握光由一种介质射入另一种介质时，在两种介质的界面上将发生光的传播方向改变的现象叫光的折射．