Question

（18分）如图所示，在坐标原点O处，能向四周均匀发射速度大小相等、方向都平行于纸面的带正电粒子。在O点右侧有一半径为R的圆形薄板，薄板中心O′位于x轴上，且与x轴垂直放置，薄板的两端M、N与原点O正好构成等腰直角三角形。已知带电粒子的质量为m，带电量为q，速率为v，重力不计。

（1）要使y轴右侧所有运动的粒子都能打到薄板MN上，可在y轴右侧加一平行于x轴的匀强电场，则场强的最小值E₀为多大？在电场强度为E₀时，打到板上的粒子动能为多大?

（2）要使薄板右侧的MN连线上都有粒子打到，可在整个空间加一方向垂直纸面向里的匀强磁场，则磁场的磁感应强度不能超过多少（用m、v、q、R表示）?若满足此条件，从O点发射出的所有带电粒子中有几分之几能打在板的左边?

Answer 1

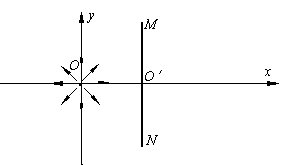
（18分）答案：（1）E₀=，E_k=；（2）磁感应强度不能超过，

解析：（1）由题意知，要使y轴右侧所有运动粒子都能打在 MN板上，其临界条件为：沿y轴方向运动的粒子作类平抛运动，且落在M或N点。

沿y轴方向，R=vt    （1分）

沿x轴方向，R=at²  （1分）

加速度    a=  （1分）

解得E₀=       （2分）

由动能定理知qE₀R=E_k－ （2分）

解得E_k=（1分）

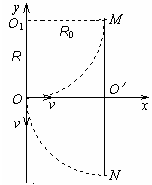
（2）加匀强磁场后，粒子沿逆时针方向做匀速圆周运动，当轨迹以O′为圆心同时过M、N两点时，轨迹直径最小（如图所示），且等于MN，即轨迹半径r=R，（3分）

由牛顿第二定律得  （2分）

解得  B=（2分）

即磁感应强度不能超过。

从O点向第四象限发射出的粒子均能打在MN板的左侧，占发射粒子总数的。（3分）