Question

【题目】如图甲所示，轻杆一端固定在O点，另一端固定一小球（可看成质点），让小球在竖直平面内做圆周运动.改变小球通过最高点时的速度大小v测 得相应的轻杆弹力F，得到F-v2图象如图乙所示，已知图线的延长线与纵轴交点坐标为（0，-b），斜率为k。不计空气阻力，重力加速度为g，则下列说法正确的是

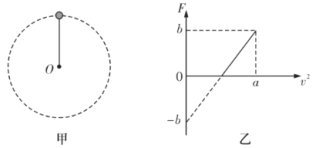
A.该小球的质量为，小球运动的轨道半径为

B.图线与横轴的交点表示小球通过最高点时所受的合外力为0

C.图线与纵轴的交点表示小球通过最高点时所受的合外力为b

D.当v2=a小球通过最高点时的向心加速度为2g

Answer 1

【答案】AD

【解析】

A．设小球运动的轨道半径为l，小球在最高点时受到拉力F和重力mg，根据牛顿第二定律可知：

解得：

结合图象可知：

mg=b

即：

斜率：

=k

解得：

A正确；

B．图线与横轴的交点表示小球通过最高点时所受的拉力为零，所受的合外力等于重力，B错误；

C．图线与纵轴的交点表示小球通过最高点时所受的支持力为所受的合外力等于0，C错误；

D．当v2=a时：

小球通过最高点时受到的合外力为2mg，向心加速度为2g，D正确。