题目内容
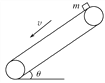
【题目】如图示，M、N为两块水平放置的平行金属板，板长为l,两板间距也为l，板间电压恒定为U。M、N左端有两竖直放置的金属板P、Q，相距为d，P、Q两板 间加的电压是6U。今有一带电量为q、质量为m的带正电粒子（重力不计）在PQ板间距离Q板d/4处由静止释放，经P、Q间的电场加速后沿M、N两板正中间垂直进入电场，最后打在距两平行板右端距离为l的竖直屏S上。
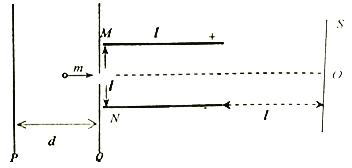
(1)粒子刚进入M、N间的偏转 电场时的速度是多少？
(2)粒子在屏上的落点距O点的距离为多少？
(3)假设大量的上述粒子以上述(1)问中的速度从MN板左端不同位置垂直进入偏转电场。试求这些粒子打到竖直屏S上的范围。
【答案】(1)
(2)
(3)距O点上方
,距O点下方
【解析】
(1) 设离Q板d/4处为A点，
，对粒子从A点到出加速电场应用动能定理：
，解得
；
(2)MN间的电场强度为：
粒子在MN电场间的加速度为：
运动时间为：
离开MN电场时偏转位移为：
，
解得：
离开MN电场时粒子速度偏转角为
粒子在屏上的落点位置：
即粒子落点距O点的距离为
；
(3)当粒子贴着M板进入MN时，由(2)得，它将偏离入射点打到屏上，即打到
，此为粒子打到屏上范围的上过界；
由(2)得
，即当粒子在距离N板
处进入MN之间，恰能从N板右边缘离开，打到屏时偏离入射点，即点以下
处。
练习册系列答案
相关题目
