题目内容
 有一个斜面,其底边固定且水平,斜面倾角在0~90°内变化,一质量为1kg的物体以初速度v0自斜面底端沿斜面上滑,滑到最高点时的位移随θ角变化的规律如图所示,则物体上滑的最小位移x和此过程中摩擦力所做的功W分别为( )
有一个斜面,其底边固定且水平,斜面倾角在0~90°内变化,一质量为1kg的物体以初速度v0自斜面底端沿斜面上滑,滑到最高点时的位移随θ角变化的规律如图所示,则物体上滑的最小位移x和此过程中摩擦力所做的功W分别为( )分析:本题的关键是根据动能定理列出表达式,将图象上两坐标点代入表达式即可求出动摩擦因数μ和
的值,然后根据数学三角代换将表达式整理为一正弦函数形式,即可讨论求解.
| v | 2 0 |
解答:解:对物体受力分析如图所示,由动能定理有-mgxsinθ-μmgxcosθ=0-
m
,及gxsinθ+μgxcosθ=
,
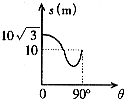
由图象可读出θ=0°时x=10
;θ=90°时x=10,代入上式可得μ=
,
=200
再将gxsinθ+μgxcosθ=
变形为gx(sinθ+μcosθ)=
,又整理为gx
sin(θ+β)=
,其中tanβ=μ=
,即β=30°
可见当sin(θ+β)=1时x最小,θ=90°-β=60°时位移最小,最小位移为x=
,代入数据可得x=5
m,所以B正确A错误
物体克服摩擦力做的功为
=μmgxcosθ=
=
×1×10×5
×cos60°=25J,所以C正确D错误.
故选BC.

| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 0 |
由图象可读出θ=0°时x=10
| 3 |
| ||
| 3 |
| v | 2 0 |
再将gxsinθ+μgxcosθ=
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 0 |
1
|
| 1 |
| 2 |
| v | 2 0 |
| ||
| 3 |
可见当sin(θ+β)=1时x最小,θ=90°-β=60°时位移最小,最小位移为x=
| ||||
g
|
| 3 |
物体克服摩擦力做的功为
| W | 克 |
| ||
| 3 |
| ||
| 3 |
| 3 |
故选BC.

点评:记住数学三角代换公式Asingθ+Bcosθ=
sin(θ+β),其中tanβ=
,在求物理极值问题中的应用.
|
| B |
| A |

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
 m
m J.
J.
 有一个斜面,其底边固定且水平,斜面倾角在0~90°内变化,一质量为1kg的物体以初速度v自斜面底端沿斜面上滑,滑到最高点时的位移随θ角变化的规律如图所示,则物体上滑的最小位移x和此过程中摩擦力所做的功W分别为( )
有一个斜面,其底边固定且水平,斜面倾角在0~90°内变化,一质量为1kg的物体以初速度v自斜面底端沿斜面上滑,滑到最高点时的位移随θ角变化的规律如图所示,则物体上滑的最小位移x和此过程中摩擦力所做的功W分别为( )
