题目内容
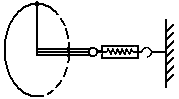
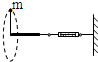 一宇航员抵达一半径为R的星球两极的表面后,为了测定该星球的质量M,做如下的实验,取一根细线穿过光滑的细直管,细线一端栓一质量为m的砝码,另一端连在一固定的测力计上,手握细线直管抡动砝码,使它在竖直平面内做半径为L的完整的圆周运动,停止抡动细直管,砝码可继续在同一竖直平面内做完整的圆周运动,且砝码恰能通过圆周运动的最高点,如图所示.此时观察得到当砝码运动到圆周最高点位置时,砝码的速度为v.
一宇航员抵达一半径为R的星球两极的表面后,为了测定该星球的质量M,做如下的实验,取一根细线穿过光滑的细直管,细线一端栓一质量为m的砝码,另一端连在一固定的测力计上,手握细线直管抡动砝码,使它在竖直平面内做半径为L的完整的圆周运动,停止抡动细直管,砝码可继续在同一竖直平面内做完整的圆周运动,且砝码恰能通过圆周运动的最高点,如图所示.此时观察得到当砝码运动到圆周最高点位置时,砝码的速度为v.已知引力常量为G,试根据题中所提供的条件和测量结果,求:
(1)该星球表面重力加速度;
(2)该星球的质量M;
(3)若将物体置于该星体的赤道处,发现它对地面的压力比在两极处时物体对地面的压力小10%,求该星体自转周期.
分析:在竖直平面内做圆周运动,恰能过通圆周的最高点,意思是在最高点时物体受到的重力完全提供向心力,即满足重力等于向心力,据此列式可得星球表面的重力加速度g,又据星球两极表面重力等于万有引力,已知星球的表面加速度和星球半径,则可得星球的质量;由题设知赤道处地面对物体的支持力,物体所受万有引力和地面的支持力的合力提供物体随星球自转的向心力,列式可得星球自转的周期.
解答: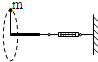 解:
解:
(1)若砝码恰能通过圆周运动的最高点,则此时绳上作用力为零,物体所受重力提供物体做圆周运动的向心力得:
mg=m
代入数据得:星球表面的重力加速度g=
(2)由于星球围绕地轴转动,故在两极处有G=F万则有:
mg=G
∴M=
=
(3)在两极处,由于地转半径为零,物体对地面的压力大小等于物体受到的万有引力,故在赤道处物体对地面的压力为两极处小10%,即物体受到地面的支持力为万有引力的90%.
又物体受到星球的万有引力和地面支持力的合力提供物体随星球自转的向心力,故有:
G
(1-0.90)=mR(
)2
T=2π
代入M=
得T=2π
答:(1)该星球表面的重力加速度为g=
(2)该星球的质量为M=
(3)该星球的自转周期为T=2π
 解:
解:(1)若砝码恰能通过圆周运动的最高点,则此时绳上作用力为零,物体所受重力提供物体做圆周运动的向心力得:
mg=m
| v2 |
| L |
代入数据得:星球表面的重力加速度g=
| v2 |
| L |
(2)由于星球围绕地轴转动,故在两极处有G=F万则有:
mg=G
| mM |
| R2 |
∴M=
| gR2 |
| G |
| v2R2 |
| GL |
(3)在两极处,由于地转半径为零,物体对地面的压力大小等于物体受到的万有引力,故在赤道处物体对地面的压力为两极处小10%,即物体受到地面的支持力为万有引力的90%.
又物体受到星球的万有引力和地面支持力的合力提供物体随星球自转的向心力,故有:
G
| Mm |
| R2 |
| 2π |
| T |
T=2π
|
| v2R2 |
| GL |
|
答:(1)该星球表面的重力加速度为g=
| v2 |
| L |
(2)该星球的质量为M=
| v2R2 |
| GL |
(3)该星球的自转周期为T=2π
|
点评:解答本题需要掌握:(1)在星球两极,物体所受的重力等于物体受到星球的万有引力;
(2)在竖直平面内做圆周运动的特殊点(最高点或最低点)物体所需向心力来源问题;
(3)自转物体向心力来源问题.
(2)在竖直平面内做圆周运动的特殊点(最高点或最低点)物体所需向心力来源问题;
(3)自转物体向心力来源问题.

练习册系列答案
相关题目
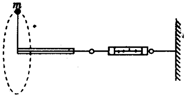
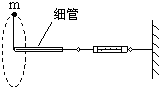 一宇航员抵达一半径为R的星球表面后,为了测定该星球的质量M,做如下的实验,取一根细线穿过光滑的细直管,细线一端栓一质量为m的砝码,另一端连在一固定的测力计上,手握细线直管抡动砝码,使它在竖直平面内做完整的圆周运动,停止抡动细直管.砝码可继续在同一竖直平面内做完整的圆周运动.如图所示,此时观察测力计得到当砝码运动到圆周的最低点和最高点两位置时,测力计的读数差为△F.已知引力常量为G,试根据题中所提供的条件和测量结果,则( )
一宇航员抵达一半径为R的星球表面后,为了测定该星球的质量M,做如下的实验,取一根细线穿过光滑的细直管,细线一端栓一质量为m的砝码,另一端连在一固定的测力计上,手握细线直管抡动砝码,使它在竖直平面内做完整的圆周运动,停止抡动细直管.砝码可继续在同一竖直平面内做完整的圆周运动.如图所示,此时观察测力计得到当砝码运动到圆周的最低点和最高点两位置时,测力计的读数差为△F.已知引力常量为G,试根据题中所提供的条件和测量结果,则( )A、该星球表面重力加速度g′=
| ||
B、该星球表面重力加速度g′=
| ||
C、该星球质量M=
| ||
D、该星球质量M=
|
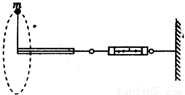
 一宇航员抵达一半径为R的星球表面后,为了测定该星球的质量M,做如下实验,取一根细线穿过光滑的细直管,细线一端栓一质量为m的砝码,另一端连在一固定的测力计上,手握细直管抡动砝码,使它在竖直平面内做完整的圆周运动.停止抡动细直管,砝码可继续在同一竖直平面做完整的圆周运动.如图所示,观察测力计得到,当砝码运动到圆周的最低点时,测力计的读数为F1;当砝码运动到圆周的最高点时,测力计的读数为F2.已知引力常量为G,试根据题中提供的条件和测量结果,求:
一宇航员抵达一半径为R的星球表面后,为了测定该星球的质量M,做如下实验,取一根细线穿过光滑的细直管,细线一端栓一质量为m的砝码,另一端连在一固定的测力计上,手握细直管抡动砝码,使它在竖直平面内做完整的圆周运动.停止抡动细直管,砝码可继续在同一竖直平面做完整的圆周运动.如图所示,观察测力计得到,当砝码运动到圆周的最低点时,测力计的读数为F1;当砝码运动到圆周的最高点时,测力计的读数为F2.已知引力常量为G,试根据题中提供的条件和测量结果,求: