题目内容
【题目】一束电子束射入如图所示的组合磁场中,其中磁场I的磁感应强度为B,方向向里,磁场横向宽度为d,纵向延伸至无穷;磁场II的磁感应强度为B,方向向外,磁场横向宽度为3d,纵向延伸至无穷。以粒子进入磁场点处为原点,射入方向为x轴正方向,建立平面直角坐标系。同时为了探测电子的位置,在磁场I的左侧边界铺设了荧光屏。已知电子的比荷为K。忽略电子间的相互作用与重力作用。求:

(1)求粒子能够进入磁场II的最小速度V1与进入区域二时的坐标。
(2)当V1满足(1)小题所给值时,当粒子速度为V2=5/3V1时离开磁场I时的坐标。
(3)当V1满足(1)小题所给值时,若运动的带电粒子能使荧光屏发光,已知放射源放出的粒子速度为3V1>V>0.5V1,那么荧光屏发光的坐标范围是多少?
【答案】(1)v1=KBd;其进入磁场II坐标为(d,-d)(2)(d,-d/3)(3)(0,-2d)到(0,4![]() R-4R)
R-4R)
【解析】(1)进入磁场II的最小速度情况如图所示:
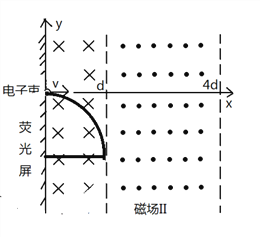
由洛伦兹力提供向心力得:ev1B=mv12/d
得v1=KBd 其进入磁场II坐标为(d,-d)
(2)电子以速度v在磁场I中运动,其运动半径r=v/KB。
当v2=5/3v1时,其轨迹半径r2=5/3r1
其运动情况如图所示:
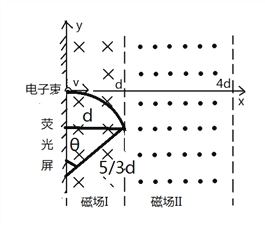
由几何关系可知,粒子偏转角θ=37°
所以离开磁场I时,粒子水平方向位移x=d,竖直方向的位移y=-(5/3d-4/3d)-d/3
离开磁场I时的坐标为(d,-d/3)
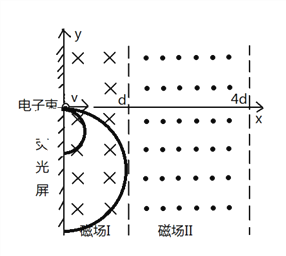
(3)当0.5v1<v<v1时,临界情况如图所示。
亮线范围是(0,-2d)到(0,-d)
当v1<v<2v1时,临界情况如图所示。
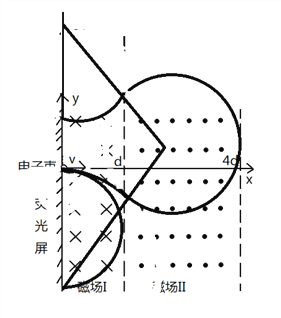
粒子达到荧光屏距离原点距离y=4![]() R-4R
R-4R
亮线范围为(0,-2d)到(0,4![]() R-4R)
R-4R)
当2v1<v<3v1时,粒子穿出区域二右边界,不能打到荧光屏上。
综上,亮线坐标范围为(0,-2d)到(0,4![]() R-4R)
R-4R)