Question

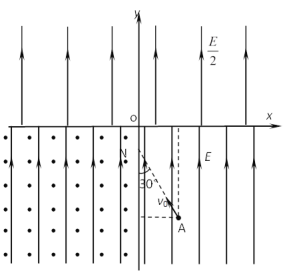
【题目】如图所示，在真空中的竖直平面内有一xoy平面直角坐标系，x轴下方有竖直向上的匀强电场，场强大小为E，且第三象限有垂直于纸面向外的水平匀强磁场；x轴上方有竖直向上的匀强电场，场强大小为。现有一电荷量的绝对值为q的带电小球，从第四象限中坐标值为（，- 2 l0） 的A点以与y轴夹角θ = 30°的速度v0斜向左上运动，恰能沿直线运动并经过y轴上的N点进入第三象限，接着垂直于x轴进入第二象限。已知重力加速度为g，求：

（1）带电小球的质量；

（2）匀强磁场的磁感应强度；

（3）带电小球从A点出发到第4次通过x轴时共经历的时间。

Answer 1

【答案】（1）；（2）；（3）（）+。

【解析】

(1)由A到N“恰能沿直线运动”，必为匀速运动，故：

mg = qE ，

得：

m =；

(2)进入第三象限后，合力等于洛伦兹力，做匀速圆周运动，由“垂直于x轴进入第二象限”及几何知识知，带电小球在磁场中做速率为v0的圆周运动的半径为：

r = l0，

又由得：

，

故 ：

；

(3)A到N的时间为：

，

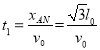从N点转过圆心角30°到达x轴的时间为：

，

带电小球进入第二象限后，做“类竖直上抛运动”，由

，

得：

(方向竖直向下) ，

在第二象限上升到最高点的时间为：

，

由对称性可知，从D回到C点所用时间为：

t4 = t3，

在第三象限中从C到P(半圆)所用时间为：

t5 =T = 6 t2 ，

设从P点进入第二象限运动至最高点Q所用时间为t6，从Q点回到P第四次通过x轴所用时间为t7，易知：

t6 = t7 = t4 = t3，

故带电小球从A点出发到第四次通过x轴时共经历的时间为：

t = t1 + t2 + t3 + t4 +t5 + t6 + t7，

即：

t =（）+。