题目内容
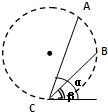（2011?徐汇区模拟）如图所示，A、B、C是同一半径为R的竖直圆周上的三个点，C为最低点，AC、BC为两条分别与水平方向成α、β角的光滑导轨．则物体分别从A、B点滑到C点所经历的时间之比1：1
1：1
，A、B点到达C点时的速率之比为| sinα |
| sinβ |
| sinα |
| sinβ |
分析：根据圆的几何知识，可以求得AC和BC的长度，由牛顿第二定律可以求得物体运动的加速度的大小，再由匀变速直线运动的规律可以求得物体运动的时间和速度的大小．
解答：解：当物体沿AC轨道运动时，对物体受力分析可知，物体在AC轨道上的合力的大小为mgsinα=ma，所以物体的加速度大小为a=gsinα，设圆的半径为R，由圆的几何关系可知，AC的长度为2Rsinα，由x=
at2可得物体由A运动到C得时间为t=
，同理可得，沿BC运动时，加速度的大小为gsinθ，BC的长度为2Rsinθ，物体由B运动到C得时间t=
，所以物体分别从A、B点滑到C点所经历的时间之比1：1；
由速度公式v=at可得，沿AC运动时，物体的速度的大小为VA=gsinα
，沿BC运动时，物体的速度的大小为VB=gsinθ
，所以A、B点到达C点时的速率之比为
．
故答案为：1：1；
．
| 1 |
| 2 |
|
|
由速度公式v=at可得，沿AC运动时，物体的速度的大小为VA=gsinα
|
|
| sinα |
| sinβ |
故答案为：1：1；
| sinα |
| sinβ |
点评：本题考查了牛顿第二定律和匀变速直线运动的规律，对物体受力分析，确定物体的运动的状态，在根据匀变速直线运动的规律来求解即可．
练习册系列答案
相关题目
（2011?徐汇区二模）如图所示，挡板垂直于斜面固定在斜面上，一滑块m放在斜面上，其上表面呈弧形且左端最薄，一球M搁在挡板与弧形滑块上，一切摩擦均不计，用平行于斜面的拉力F拉住弧形滑块，使球与滑块均静止，现将滑块平行于斜面向上拉过一较小的距离，球仍搁在挡板与滑块上且仍处于静止状态，则与原来相比（ ）
（2011?徐汇区二模）如图所示，两端封闭、粗细均匀的U形管，两边封有理想气体，U形管处于竖直平面内，且上管置于容器A中，下管置于容器B中，设A中初温为TA，B中初温为TB，此时下管水银比上管水银长了L，若同时将A、B温度升高△T，重新稳定后，则（ ）
（2011?徐汇区二模）如图所示，螺线管内有一平行于轴线的匀强磁场，规定图中箭头所示方向为磁感应强度B的正方向，螺线管与U型导线框cdef相连，导线框cdef内有一半径很小的金属圆环L，圆环与导线框cdef在同一平面内．当螺线管内的磁感应强度随时间按图示规律变化时（ ）