Question

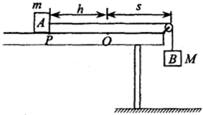
如图所示，水平桌面右端固定一光滑定滑轮，O点到定滑轮的距离s=0.5m，当用竖直向下的力将质量m=0.2kg的木块A按住不动时，质量M=0.3kg的重物B刚好与地面接触（对地面无压力），木块与桌面间的动摩擦因数为0.5．然后将木块A拉到P点，OP间的距离为h=0.5m，待B稳定后由静止释放，g取10m/s²．求：

（1）木块A按住不动时所受摩擦力；

（2）木块A由静止释放后运动到O点时的速度大小；

（3）通过计算说明木块A是否会撞到定滑轮？若不会撞上请求出最终木块A停在距定滑轮多远的地方；若会撞上，请定性说出两种避免撞上的解决方案．

 

 

Answer 1

【答案】

(1) 3N，方向水平向左(2) 2m/s (3) 木块A不会撞到定滑轮；停在距定滑轮0.1m处

【解析】

试题分析：（1）木块A按住不动时所受摩擦力为静摩擦力，由平衡条件得f=T=Mg=3N，方向水平向左。

（2）在B下落至地面前，据动能定理，有

Mgh﹣μmgh=（M+m）v²，

得v==2m/s

（3）在B落地后，A运动到停下来，设A继续向右滑行距离为s′时停下，则据动能定理，有﹣μmgs′=0﹣mv²

得 s′==0.4m＜0.5m        

所以木块A不会撞到定滑轮，最终木块A停在距定滑轮0.1m处．

考点：此题考查的是动能定理。