题目内容
【题目】如图所示,光滑绝缘的正方形水平桌面边长为d="0.48" m,离地高度h="1.25" m。桌面上存在一水平向左的匀强电场(除此之外其余位置均无电场),电场强度E=l×l0![]() N/C。在水平桌面上某一位置P处有一质量m=" 0.01" kg,电量q=l×10
N/C。在水平桌面上某一位置P处有一质量m=" 0.01" kg,电量q=l×10![]() C的带正电小球以初速v0="1" m/s向右运动。空气阻力忽略不计,重力加速度g=10
C的带正电小球以初速v0="1" m/s向右运动。空气阻力忽略不计,重力加速度g=10![]() 。求:
。求:
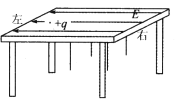
(1)小球在桌面上运动时加速度的大小和方向?
(2)P处距右端桌面多远时,小球从开始运动到最终落地的水平距离最大?并求出该最大水平距离?
【答案】(1)1.0m/s2,水平向左;(2)距桌面右端![]() 处放入,有最大水平距离为
处放入,有最大水平距离为![]()
【解析】试题分析:(1)对小球受力分析,受到重力、支持力和电场力,重力和支持力平衡,根据牛顿第二定律,有![]() 方向:水平向左
方向:水平向左
(2)球先向右减速,假设桌面足够长,减为零的过程,有![]() ,大于桌面边长,故小球一直减速;设球到桌面右边的距离为x1,球离开桌面后作平抛运动的水平距离为x2,则x总=x1+x2
,大于桌面边长,故小球一直减速;设球到桌面右边的距离为x1,球离开桌面后作平抛运动的水平距离为x2,则x总=x1+x2
由v2-v02=-2ax1
代入得![]() ;设平抛运动的时间为t,根据平抛运动的分位移公式,有
;设平抛运动的时间为t,根据平抛运动的分位移公式,有
h=![]() gt2代入得t=0.5s
gt2代入得t=0.5s
水平方向,有x2=vt=0.5![]()
故 x总=x1+0.5![]()
令y=![]()
则 x总=![]() ,故,当y=
,故,当y=![]() ,即x1=
,即x1=![]() 时,水平距离最大,最大值为:xm=
时,水平距离最大,最大值为:xm=![]() ,即距桌面右端
,即距桌面右端![]() 处放入,有最大水平距离为
处放入,有最大水平距离为![]() 。
。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目