题目内容
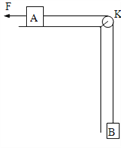
【题目】如图所示,在水平桌面的边角处有一轻质光滑的定滑轮K,一条不可伸长的轻绳绕过定滑轮K分别与物体A、B相连,A、B的质量分别为mA=3kg、mB=2kg.现用一水平恒力F拉物体A,使物体B上升(A、B均从静止开始运动).已知当B上升距离为h=0.2m时,B的速度为v=1m/s.已知A与桌面的动摩擦因数μ=0.25,重力加速度为g=10m/s2。求:
(1)力F的大小和A、B系统的加速度大小.
(2)当B的速度为v=1m/s时,轻绳突然断了,那么在B上升的过程中,A向左运动多远?
【答案】(1)40N,2.5 m/s2(2)0.15m
【解析】试题分析:(1)物体B匀加速上升,根据速度位移公式,有:a=![]() =2.5m/s
=2.5m/s
对A运用牛顿第二定律,得到:F-μmAg-T=mAa
对B运用牛顿第二定律,得到:T-mBg=mBa
联立解得:F=40N
即力F的大小为40N,A、B系统的加速度大小为2.5m/s2.
(2)细线断开后,B物体由于惯性继续上升,根据速度时间公式,有:t=V/g=0.1s ①
对A运用牛顿第二定律,得到:F-μmAg=mAa'②
物体A做匀加速直线运动,根据速度时间公式,有S=vt+1/2a′t2③
由①②③解得S=0.15m
即当B的速度为v=1m/s时突然线断了,在B上升的过程中,A向左运动0.15m.

练习册系列答案
相关题目