题目内容
5.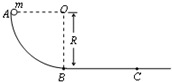 如图所示,AB是竖直平面内的四分之一圆弧轨道,在下端B与水平直轨道相切,一小球自A点由静止开始沿轨道下滑,已知圆轨道半径为R,小球到达B点时的速度为v,则小球在B点受2个力的作用,这几个力的合力的方向是竖直向上,小球在B点的加速度大小为$\frac{{v}^{2}}{R}$,方向是竖直向上.(不计一切阻力)
如图所示,AB是竖直平面内的四分之一圆弧轨道,在下端B与水平直轨道相切,一小球自A点由静止开始沿轨道下滑,已知圆轨道半径为R,小球到达B点时的速度为v,则小球在B点受2个力的作用,这几个力的合力的方向是竖直向上,小球在B点的加速度大小为$\frac{{v}^{2}}{R}$,方向是竖直向上.(不计一切阻力)
分析 由于不计一切阻力,所以小球只受到重力和支持力的作用,两个力的合力提供向心力,然后结合牛顿第二定律即可求出.
解答 解:由于不计一切阻力,所以小球只受到重力和支持力的2个力的作用;
小球刚刚到达B时,仍然在圆轨道上,重力与支持力的合力提供向上的向心力,所以合力的方向向上,根据牛顿第二定律可知,加速度的方向也向上.根据向心力的表达式可知,小球的向心加速度:
$a=\frac{{v}^{2}}{R}$
故答案为:2,竖直向上,$\frac{{v}^{2}}{R}$,竖直向上
点评 本题考查了圆周运动的向心力的来源,能正确减小受力分析,记住向心力与向心加速度的表达式即可正确解答.基础题目.

练习册系列答案
相关题目
14.做初速度为零的匀加速直线运动的物体,由静止开始,通过连续三段位移之比为1:3:5,则通过这三段位移的时间之比和分别通过三段位移末时的速度之比是( )
| A. | 1:2:3,1:3:5 | B. | 1:4:9,1:2:3 | C. | 1:1:1,1:2:3 | D. | 1:1:1,1:4:9 |
15. 如图所示,在光滑小滑轮C正下方相距h的A处固定一电量为Q的点电荷,电量为q的带电小球B,用绝缘细线拴着,细线跨过定滑轮,另一端用适当大小的力拉住,使小球处于静止状态,这时小球与A点的距离为R,细线CB与AB垂直.(静电力恒量为k,环境可视为真空),若小球所受的重力的为 G,缓慢拉动细线(始终保持小球平衡)直到小球刚到滑轮的正下方过程中,拉力所做的功为W1,电场力做功为W2,则下列关系式正确的是( )
如图所示,在光滑小滑轮C正下方相距h的A处固定一电量为Q的点电荷,电量为q的带电小球B,用绝缘细线拴着,细线跨过定滑轮,另一端用适当大小的力拉住,使小球处于静止状态,这时小球与A点的距离为R,细线CB与AB垂直.(静电力恒量为k,环境可视为真空),若小球所受的重力的为 G,缓慢拉动细线(始终保持小球平衡)直到小球刚到滑轮的正下方过程中,拉力所做的功为W1,电场力做功为W2,则下列关系式正确的是( )
 如图所示,在光滑小滑轮C正下方相距h的A处固定一电量为Q的点电荷,电量为q的带电小球B,用绝缘细线拴着,细线跨过定滑轮,另一端用适当大小的力拉住,使小球处于静止状态,这时小球与A点的距离为R,细线CB与AB垂直.(静电力恒量为k,环境可视为真空),若小球所受的重力的为 G,缓慢拉动细线(始终保持小球平衡)直到小球刚到滑轮的正下方过程中,拉力所做的功为W1,电场力做功为W2,则下列关系式正确的是( )
如图所示,在光滑小滑轮C正下方相距h的A处固定一电量为Q的点电荷,电量为q的带电小球B,用绝缘细线拴着,细线跨过定滑轮,另一端用适当大小的力拉住,使小球处于静止状态,这时小球与A点的距离为R,细线CB与AB垂直.(静电力恒量为k,环境可视为真空),若小球所受的重力的为 G,缓慢拉动细线(始终保持小球平衡)直到小球刚到滑轮的正下方过程中,拉力所做的功为W1,电场力做功为W2,则下列关系式正确的是( )| A. | W1=$\frac{mg}{2h}$(h2-R2) | B. | W2=GR(1-$\frac{R}{h}$) | C. | W1=$\frac{hkQq}{{R}^{2}}$(1-$\frac{R}{h}$) | D. | G=$\frac{khQq}{{R}^{3}}$ |

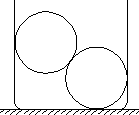 如图所示,两个重均为G=100N,半径r=5cm的光滑球,放在底面半径为R=9cm的圆筒内.试求球与球、球与筒壁及球与筒底间相互作用的弹力的大小.
如图所示,两个重均为G=100N,半径r=5cm的光滑球,放在底面半径为R=9cm的圆筒内.试求球与球、球与筒壁及球与筒底间相互作用的弹力的大小.
 为了测定光在透明有机玻璃中的传播速度,实验室提供的器材有:矩形有机玻璃砖、木板、刻度尺、三角板、白纸、大头针.已知真空中的光速C.
为了测定光在透明有机玻璃中的传播速度,实验室提供的器材有:矩形有机玻璃砖、木板、刻度尺、三角板、白纸、大头针.已知真空中的光速C.