题目内容
6.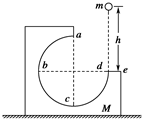 如图所示,M为固定在水平桌面上的有缺口的正方形木块,abcd为半径是R的$\frac{3}{4}$光滑圆弧形轨道,a为轨道的最高点,de面水平且长度也为R,将质量为m的小球在d点的正上方高为h处由静止释放,让其自由下落到d处沿切线进入轨道内运动,不计空气阻力,则( )
如图所示,M为固定在水平桌面上的有缺口的正方形木块,abcd为半径是R的$\frac{3}{4}$光滑圆弧形轨道,a为轨道的最高点,de面水平且长度也为R,将质量为m的小球在d点的正上方高为h处由静止释放,让其自由下落到d处沿切线进入轨道内运动,不计空气阻力,则( )| A. | 只要h大于r,释放后小球就能通过a点 | |
| B. | 只要改变h的大小,就能使小球通过a点后,既可能落回轨道内,又可能落到de面上 | |
| C. | 无论怎样改变h的大小,都不可能使小球通过a点后落回轨道内 | |
| D. | 调节h的大小,不能使小球飞出de面之外(即e的右侧) |
分析 根据牛顿第二定律分析小球的加速度与质量的关系.若小球恰能通过a点,其条件是小球的重力提供向心力,根据牛顿第二定律可解得小球此时的速度,用平抛运动的规律:水平方向的匀速直线运动,竖直方向的自由落体运动规律求出水平距离,由机械能守恒定律可求得h,分析小球能否通过a点后落回轨道内.
解答 解:A、小球恰能通过a点的条件是小球的重力提供向心力,根据牛顿第二定律:
mg=m$\frac{{v}^{2}}{R}$
解得:v=$\sqrt{gR}$
根据动能定理:mg(h-R)=$\frac{1}{2}$mv2
得:h=1.5R
可知只有满足h≥1.5R,释放后小球才能通过a点,故A错误;
BCD、小球离开a点时做平抛运动,用平抛运动的规律,
水平方向的匀速直线运动:x=vt
竖直方向的自由落体运动:R=$\frac{1}{2}$gt2,
解得:x=$\sqrt{2}$R>R,故无论怎样改变h的大小,都不可能使小球通过a点后落回轨道内,小球将通过a点不可能到达d点.只要改变h的大小,就能改变小球到达a点的速度,就有可能使小球通过a点后,落在de之间或之外.故BD错误,C正确.
故选:C.
点评 本题实质是临界问题,要充分挖掘临界条件,要理解平抛运动的规律:水平方向的匀速直线运动,竖直方向的自由落体运动.

练习册系列答案
相关题目
13.甲物体的质量是乙物体的5倍,它们在同一高度同时开始自由下落,最后落在同一个水平面上,忽略空气的阻力,则下列说法中正确的是( )
| A. | 甲、乙同时落地 | B. | 甲比乙先落地 | ||
| C. | 甲比乙先落地 | D. | 下落过程中,甲的加速度是乙的5倍 |
14.不同时代的学者或科学家对运动有不同的描述,下列三位学者或科学家生活年代先后顺序正确的是( )
| A. | 爱因斯坦、牛顿、亚里士多德 | B. | 牛顿、亚里士多德、爱因斯坦 | ||
| C. | 亚里士多德、爱因斯坦、牛顿 | D. | 亚里士多德、牛顿、爱因斯坦 |
18.关于摩擦力,下列说法正确的是( )
| A. | 静摩擦力产生在两个静止的物体之间,滑动摩擦力产生在两个运动的物体之间 | |
| B. | 有摩擦力一定存在弹力,且摩擦力的方向总与相对应的弹力方向垂直 | |
| C. | 静摩擦力可以作为动力、阻力,而滑动摩擦力只能作为阻力 | |
| D. | 摩擦力的大小与正压力大小成正比 |
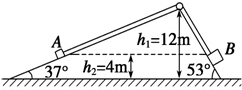 如图所示,一个截面为劈形的滑梯固定在水平地面上,高h1=12m,底角分别为37°、53°,将A、B两物块(其质量mA=mB=2kg)用轻绳连续,通过滑梯顶端的小滑轮跨放在左右两侧斜面上,开始时在滑轮处压住轻绳,已知轻绳伸直时,两物块离地高度相等并且h2=4m.不计一切摩擦力,取g=10m/s2,sin37°=0.6,sin53°=0.8.
如图所示,一个截面为劈形的滑梯固定在水平地面上,高h1=12m,底角分别为37°、53°,将A、B两物块(其质量mA=mB=2kg)用轻绳连续,通过滑梯顶端的小滑轮跨放在左右两侧斜面上,开始时在滑轮处压住轻绳,已知轻绳伸直时,两物块离地高度相等并且h2=4m.不计一切摩擦力,取g=10m/s2,sin37°=0.6,sin53°=0.8.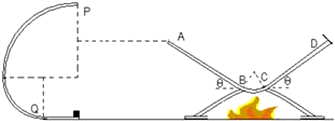
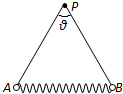 两根长度均为d=0.25m的细绳,一端系着质量均为m=0.4kg的小球A、B,另一端固定在P点,如图所示.A、B之间连接有原长l0=0.4m的轻弹簧.静止时AP、BP之间的夹角θ=74°,弹簧呈水平.g=10m/s2.求:弹簧的劲度系数k.
两根长度均为d=0.25m的细绳,一端系着质量均为m=0.4kg的小球A、B,另一端固定在P点,如图所示.A、B之间连接有原长l0=0.4m的轻弹簧.静止时AP、BP之间的夹角θ=74°,弹簧呈水平.g=10m/s2.求:弹簧的劲度系数k.