题目内容
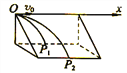
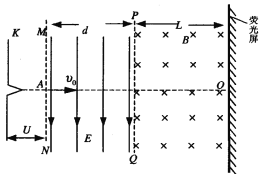
【题目】如图所示,K与虚线MN之间是加速电场。虚线MN与PQ之间是匀强电场,虚线PQ 与荧光屏之间是匀强磁场,且MN、PQ与荧光屏三者互相平行。电场和磁场的方向如图所示,图中A点与O点的连线垂直于荧光屏。一带正电的粒子经加速电场由静止加速后从A点离开加速电场,垂直于偏转电场方向射入偏转电场,在离开偏转电场后进入匀强磁场,最后恰好垂直地打在荧光屏上。已知电场和磁场区域在竖直方向足够长,加速电场电压与偏转电场的场强关系为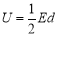 ,式中的
,式中的![]() 是偏转电场的宽度,磁感应强度B与速度V0关系符合表达式
是偏转电场的宽度,磁感应强度B与速度V0关系符合表达式![]() ,若题中只有偏转电场的宽度
,若题中只有偏转电场的宽度![]() 为已知量,(粒子重力不计)则:
为已知量,(粒子重力不计)则:
(1)画出带电粒子轨迹示意图;
(2)磁场的宽度 L 为多少?
(3)带电粒子在电场和磁场中垂直于V0方向的偏转距离分别是多少?
【答案】(1)轨迹如图;(2)d(3)在偏转电场中距离0.5d;在磁场中偏转距离为0.414d;
【解析】
试题分析:(1)粒子先做加速,再做类平抛运动,最后做圆周运动,垂直打在板上,轨迹如下图所示:
(2)粒子在加速电场中,由动能定理可知:Uq=![]() mv02
mv02
粒子在匀强电场中做类平抛运动,设偏转角为θ,有![]()
vy=at
![]()
![]()
U=![]() Ed
Ed
解得:θ=45°
带电粒子离开电场偏转电场的速度为![]() v0;
v0;
粒子在磁场中运动,由牛顿第二定律有:![]()
在磁场中偏转的半径为
由图可知,磁场宽度L=Rsinθ=d
(3)由图中几何关系可知,带电粒子在偏转电场中距离y1=0.5d;在磁场中偏转距离为R-Rcosθ=0.414d;

练习册系列答案
相关题目