题目内容
 如图所示,重量为G的均匀链条,两端用等长的轻绳连接挂在等高的地方,绳与水平线成θ角,试求:
如图所示,重量为G的均匀链条,两端用等长的轻绳连接挂在等高的地方,绳与水平线成θ角,试求:(1)绳子的张力:
(2)链条最低点的张力.
分析:(1)对链条受力分析,受重力和两个拉力,然后根据平衡条件并运用合成法求解;
(2)对左半边链条受力分析,受重力、拉力和右半边链条的拉力,根据平衡条件并运用合成法求解.
(2)对左半边链条受力分析,受重力、拉力和右半边链条的拉力,根据平衡条件并运用合成法求解.
解答:解:(1)对链条受力分析,受重力和两个拉力,如图所示:

根据平衡条件,有:T=
=
(2)对左半边链条受力分析,受重力、拉力和右半边链条的拉力,如图所示:
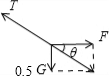
由平衡条件可得:F=
cotθ
答:(1)绳子的张力为
;
(2)链条最低点的张力为
cotθ.

根据平衡条件,有:T=
| ||
| sinθ |
| G |
| 2sinθ |
(2)对左半边链条受力分析,受重力、拉力和右半边链条的拉力,如图所示:

由平衡条件可得:F=
| G |
| 2 |
答:(1)绳子的张力为
| G |
| 2sinθ |
(2)链条最低点的张力为
| G |
| 2 |
点评:本题关键是对链条受力分析,然后根据平衡条件列式求解,要注意三力平衡时,三力不平行时一定是共点力.

练习册系列答案
相关题目
 如图所示,重量为G的物体A在大小为F的水平向左恒力作用下,静止在倾角为α的光滑斜面上.下列关于物体对斜面压力N大小的表达式,不正确的是( )
如图所示,重量为G的物体A在大小为F的水平向左恒力作用下,静止在倾角为α的光滑斜面上.下列关于物体对斜面压力N大小的表达式,不正确的是( ) 如图所示,重量为G的物体A在大小为F的水平向左的恒力作用下静止在倾角为α的固定光滑斜面上.下列关于物体对斜面压力FN大小的表达式,正确的是( )
如图所示,重量为G的物体A在大小为F的水平向左的恒力作用下静止在倾角为α的固定光滑斜面上.下列关于物体对斜面压力FN大小的表达式,正确的是( ) 如图所示,重量为G的物块在推力F的作用下,沿水平面向右匀速运动,则关于物块的受力分析正确的是( )
如图所示,重量为G的物块在推力F的作用下,沿水平面向右匀速运动,则关于物块的受力分析正确的是( )



