题目内容
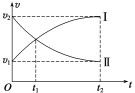
【题目】如图甲所示,质量为m=0.4kg可视为质点的物块静止放在水平地面上,物块与地面间的动摩擦因数为0.2,且最大静摩擦力等于滑动摩擦力。距离物块S=7.5m处有一光滑半圆轨道,轨道最低点P的切线水平。t=0时用水平拉力F由静止拉动物块,使物块沿水平地面向半圆轨道做加速运动。物体的速度v与拉力F大小倒数的v—![]() 图象如图乙所示,AB平行于v轴,BC反向延长过原点O。物块运动过程中0~t1时间内对应图线中的线段AB,t1~t2时间内对应图线中的线段BC,时刻t2=1s,t2时刻后撤掉拉力。重力加速度取g=10m/s2。
图象如图乙所示,AB平行于v轴,BC反向延长过原点O。物块运动过程中0~t1时间内对应图线中的线段AB,t1~t2时间内对应图线中的线段BC,时刻t2=1s,t2时刻后撤掉拉力。重力加速度取g=10m/s2。
(1)0~t1时间内物块的位移大小;
(2)物块能够经过半圆轨道最高点Q,半圆轨道的半径R满足什么条件?
(3)物块经半圆轨道最高点Q后抛出落回地面,落地后不再弹起。圆轨道半径R多大时物块落点离P点的距离最大,最大值为多少?

【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,
,![]()
【解析】
(1)物块在![]() 时间内做匀加速运动,发生位移为
时间内做匀加速运动,发生位移为![]() ,则有
,则有
![]()
![]()
联立解得
![]()
(2)由运动学公式可得
![]()
由题意知
![]()
物块在![]() 时间内做变速运动位移为
时间内做变速运动位移为![]() ,由动能定理得
,由动能定理得
![]()
撤去外力后,物块做匀减速运动,根据牛顿第二定律可得
![]()
![]()
物块能够达到圆轨道的最高点,则有
![]()
物块从P点到Q点,机械能守恒,因此有
![]()
代入数据解得
![]()
综上所述,R应满足条件
![]()
(3)物块到达圆轨道最高点的速度为![]() ,则有
,则有
![]()
物块离开Q点做平抛运动,因此可得
![]()
![]()
联立可得
![]()
因此,当![]() 时,可算得
时,可算得
![]()

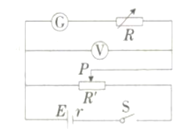
【题目】某实验小组利用如图所示的实验电路来测量电阻的阻值,Rx为待测电阻。

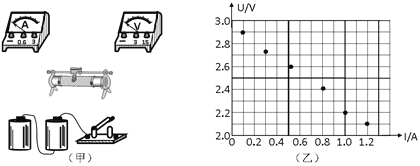
(1)闭合开关S,单刀双掷开关S2接至1,适当调节滑动变阻器R0后保持其阻值不变。改变电阻箱的阻值R,得到一组电压表的示数U与R的数据如下表:
电阻R/Ω | 5.0 | 10.0 | 15.0 | 25.0 | 35.0 | 45.0 |
电压U/V | 1.00 | 1.50 | 1.80 | 2.14 | 2.32 | 2.45 |
请根据实验数据作出U—R关系图象_________;

(2)开关S2切换至2,读出电压表示数,利用(1)中测绘的U—R图象即可得出被测电阻的阻值。若某次测量时,电压表示数为2.00V,可得Rx=___________Ω;(保留2位有效数字)
(3)使用较长时间后,电池的电动势可认为不变,但内阻增大。若仍用本实验装置和(1)中测绘的U—R图象测定某一电阻,则测定结果将___________(选填“偏大”或“偏小”)。现将开关S2接至1,将电阻箱R的阻值调为5.0Ω,你应如何调节滑动变阻器R0,便仍可利用本实验装置和(1)中测绘的U—R图象实现对待测电阻进行准确测量?______________________。