Question

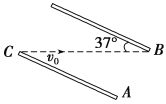
【题目】如图所示，有一对长4 cm的平行金属板，相距3 cm倾斜放置与水平面成37°角，两板间加上50 V电压，有一带电粒子质量为4×10－8 kg，以1 m/s的速度自A板左边缘C水平进入电场，在电场中沿水平方向运动并恰好从B板边缘水平飞出，虚线为其运动轨迹，g＝10 m/s2，sin 37°＝0.6.求：

(1)带电粒子所带电量；

(2)带电粒子飞出电场时的速度．

Answer 1

【答案】①带电粒子所带电量3×10﹣10C．

②带电粒子飞出电场时的速度m/s．

【解析】

试题①带电粒子做直线运动，对粒子进行受力分析，粒子在竖直方向受到的合力为零，由平衡条件可以求出粒子所带电量；

②由动能定理可以求出粒子飞出电场时的速度大小．

解：①对带电粒子受力分析，如图所示

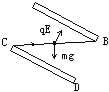
因带电粒子水平方向沿直线运动

∴mg=qEcos37°，又E=，

解得：q===3×10﹣10C；

②令带电粒子飞出电场时速度为v，

由动能定理得：qu=mv2﹣mv02，

解得：v=m/s；

答：①带电粒子所带电量3×10﹣10C．

②带电粒子飞出电场时的速度m/s．