题目内容
4.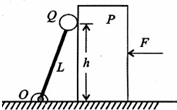 如图所示,在光滑的水平地面上有一个表面光滑的物块P,它的质量为M,一长为L的轻杆下端用光滑铰链连接于O点,O点固定于地面上,轻杆的上端连接着一个可视为质点的小球Q,它的质量为m,且M=5m.开始时,小球斜靠在物块左侧,它距地面的高度为h,物块右侧受到水平向左推力F的作用,整个装置处于静止状态.若现在撤去水平推力F,则下列说法中正确的是( )
如图所示,在光滑的水平地面上有一个表面光滑的物块P,它的质量为M,一长为L的轻杆下端用光滑铰链连接于O点,O点固定于地面上,轻杆的上端连接着一个可视为质点的小球Q,它的质量为m,且M=5m.开始时,小球斜靠在物块左侧,它距地面的高度为h,物块右侧受到水平向左推力F的作用,整个装置处于静止状态.若现在撤去水平推力F,则下列说法中正确的是( )| A. | 物块先做匀加速运动,后做匀速运动 | |
| B. | 在小球和物块分离前,当轻杆与水平面的夹角为θ时,小球的速度大小$\sqrt{\frac{2g(h-Lsinθ)}{{1+5si{n^2}θ}}}$ | |
| C. | 小球与物块分离时,小球一定只受重力作用 | |
| D. | 在小球落地之前,小球的机械能一直减少 |
分析 当立方体的速度大于小球在水平方向的速度时,立方体和小球分离,在分离之前,小球和立方体的水平方向速度相同,由能量守恒定律可以判断AB,在分离之前,立方体一直向右加速运动,小球的速度也增大,合外力做正功,分离后,只有重力做功,机械能守恒.
解答 解:A、假设立方体和地面之间有摩擦力,若摩擦力太大,则小球不会推动立方体运动,如摩擦力太小,立方体会在小球落在水平地面上之前离开小球;若摩擦力适中,小球恰好在落到水平地面后与立方体分离.由于物块P与地面间没有摩擦,故P物体会在小球落在水平地面上之前离开小球,故物块先做加速运动(不一定是匀加速),后做匀速运动,故A错误;
B、在小球和物块分离前,当轻杆与水平面的夹角为θ时,由能量守恒定律有:
mg(h-Lsinθ)=$\frac{1}{2}m{v}_{P}^{2}+\frac{1}{2}m{v}_{Q}^{2}$ ①
将小球的速度沿着水平方向和竖直方向正交分解,有:
vP=vQsinα ②
联立解得:
vQ=$\sqrt{\frac{2g(h-Lsinθ)}{1+5si{n}^{2}θ}}$
故B正确;
C、对小球和立方体整体受力分析,受重力、杆的弹力T、支持力,在水平方向运用牛顿第二定律,有:Tcosα=(m+M)ax,刚分离时加速度的水平分量为零,故杆的弹力为零,故小球只受重力;故C正确;
D、在分离之前,小球的机械能减小,分离后,只有重力做功,机械能守恒,故D错误;
故选:BC.
点评 本题关键是找到小球的分运动和合运动,知道当立方体的速度大于小球在水平方向的速度时,立方体和小球分离,在分离之前,小球和立方体的水平方向速度相同,难度适中.

练习册系列答案
相关题目
19.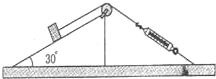 如图所示,斜面的角为30°,质量为M=2kg,有一质量m=1.0kg的物体放在斜面上用细绳相连.细绳的一端跨过摩擦不计的定滑轮与固定的轻弹簧秤相连.斜面和物体均静止在水平地面上,弹簧秤的示数为4.9N.关于物体受力的判断(取g=9.8m/s2),下列说法正确的是( )
如图所示,斜面的角为30°,质量为M=2kg,有一质量m=1.0kg的物体放在斜面上用细绳相连.细绳的一端跨过摩擦不计的定滑轮与固定的轻弹簧秤相连.斜面和物体均静止在水平地面上,弹簧秤的示数为4.9N.关于物体受力的判断(取g=9.8m/s2),下列说法正确的是( )
 如图所示,斜面的角为30°,质量为M=2kg,有一质量m=1.0kg的物体放在斜面上用细绳相连.细绳的一端跨过摩擦不计的定滑轮与固定的轻弹簧秤相连.斜面和物体均静止在水平地面上,弹簧秤的示数为4.9N.关于物体受力的判断(取g=9.8m/s2),下列说法正确的是( )
如图所示,斜面的角为30°,质量为M=2kg,有一质量m=1.0kg的物体放在斜面上用细绳相连.细绳的一端跨过摩擦不计的定滑轮与固定的轻弹簧秤相连.斜面和物体均静止在水平地面上,弹簧秤的示数为4.9N.关于物体受力的判断(取g=9.8m/s2),下列说法正确的是( )| A. | 地面对斜面体的摩擦力大小为零 | |
| B. | 斜面对物体的摩擦力大小不为零 | |
| C. | 地面 对斜面的支持力大于29.4N,方向垂直地面向上 | |
| D. | 地面对物体的支持力小于29.4N,方向垂直地面向上 |
20.做匀速圆周运动的物体,下列物理量变化的是( )
| A. | 线速度 | B. | 速率 | C. | 频率 | D. | 周期 |
17.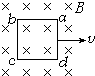 如图所示,闭合矩形线框abcd位于磁感应强度为B的匀强磁场中,ad边位于磁场边缘,线框平面与磁场垂直,ab、ad边长分别用L1、L2表示,线圈总电阻为R,若把线圈沿v方向匀速拉出磁场所用时间为△t,则通过线框导线截面的电量是( )
如图所示,闭合矩形线框abcd位于磁感应强度为B的匀强磁场中,ad边位于磁场边缘,线框平面与磁场垂直,ab、ad边长分别用L1、L2表示,线圈总电阻为R,若把线圈沿v方向匀速拉出磁场所用时间为△t,则通过线框导线截面的电量是( )
 如图所示,闭合矩形线框abcd位于磁感应强度为B的匀强磁场中,ad边位于磁场边缘,线框平面与磁场垂直,ab、ad边长分别用L1、L2表示,线圈总电阻为R,若把线圈沿v方向匀速拉出磁场所用时间为△t,则通过线框导线截面的电量是( )
如图所示,闭合矩形线框abcd位于磁感应强度为B的匀强磁场中,ad边位于磁场边缘,线框平面与磁场垂直,ab、ad边长分别用L1、L2表示,线圈总电阻为R,若把线圈沿v方向匀速拉出磁场所用时间为△t,则通过线框导线截面的电量是( )| A. | $\frac{{B{L_1}{L_2}}}{R△t}$ | B. | $\frac{{B{L_1}{L_2}}}{R}$ | C. | $\frac{{B{L_1}{L_2}}}{△t}$ | D. | BL1L2 |
16.声波在水中的速度大于在空气中的速度,让某一波源发出的声波通过空气和水中的相同的小孔,下列说法正确的是( )
| A. | 在水中的波长大于在空气中的波长,在水中更容易出现衍射现象 | |
| B. | 在水中的波长小于在空气中的波长,在水中更容易出现衍射现象 | |
| C. | 在水中的波长大于在空气中的波长,在空气中更容易出现衍射现象 | |
| D. | 在水中的波长小于在空气中的波长,在空气中更容易出现衍射现象 |
14.“嫦娥三号”探测器在到达距离月球100m高度时,会在自主发动机的控制下进行短暂悬停.然后“嫦娥三号”在反推火箭的作用下慢慢下降,到距离月球4m高度再次悬停.最后,关掉发动机,自由下落到月球表面.下列判断不正确的是( )
| A. | “嫦娥三号”在整个落月过程中相对于月球的机械能减少 | |
| B. | “嫦娥三号”在处于悬停阶段时相对于月球的加速度为零 | |
| C. | “嫦娥三号”在关闭发动机自由下落到月球表面过程中,用时约为0.9s | |
| D. | “嫦娥三号”从100m悬停点下降到4m悬停点的过程中,合外力做功为零 |
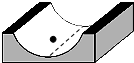 一同学在半径为1m的光滑圆弧面内做测定重力加速度的实验(如图所示).他用一个直径为0.02m质量分布均匀的光滑实心球.操作步骤如下:
一同学在半径为1m的光滑圆弧面内做测定重力加速度的实验(如图所示).他用一个直径为0.02m质量分布均匀的光滑实心球.操作步骤如下: