题目内容
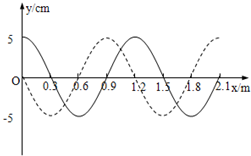 如图所示,实线和虚线分别是沿x轴传播的一列简谐横波在t=0和t=0.06s时刻的波形图.已知在t=0时刻,x=1.5m处的质点向y轴正方向运动.
如图所示,实线和虚线分别是沿x轴传播的一列简谐横波在t=0和t=0.06s时刻的波形图.已知在t=0时刻,x=1.5m处的质点向y轴正方向运动.①判断该波的传播方向;
②求该波的最小频率;
③若3T<t<4T,求该波的波速.
分析:①已知在t=0时刻,x=1.5m处的质点向y轴正方向运动,根据波形平移法得到该波的传播方向;
②由两个时刻的波形可知时间与周期的关系,求出周期的通项,即可求得频率的通项,从而求出频率的最小值.
③根据上题的结论,求解频率的特殊值,读出波长,求出波速.
②由两个时刻的波形可知时间与周期的关系,求出周期的通项,即可求得频率的通项,从而求出频率的最小值.
③根据上题的结论,求解频率的特殊值,读出波长,求出波速.
解答:解:①已知在t=0时刻,x=1.5m处的质点向y轴正方向运动,波形向右平移,所以该波向右传播.
②由图得:△t=(n+
)T,得:T=
=
=
s(n=0,1,2,…)
解得:频率的通项为f=
=
Hz,
当n=0,f=12.5Hz为最小频率.
③当3T<t<4T时,上题中:n=3
则波速为:v=λf=1.2×
=75m/s
答:
①该波向右传播;
②该波的最小频率为12.5Hz;
③若3T<t<4T,该波的波速为75m/s.
②由图得:△t=(n+
| 3 |
| 4 |
| 4△t |
| 4n+3 |
| 4×0.06 |
| 4n+3 |
| 0.24 |
| 4n+3 |
解得:频率的通项为f=
| 1 |
| T |
| 4n+3 |
| 0.24 |
当n=0,f=12.5Hz为最小频率.
③当3T<t<4T时,上题中:n=3
则波速为:v=λf=1.2×
| 15 |
| 0.24 |
答:
①该波向右传播;
②该波的最小频率为12.5Hz;
③若3T<t<4T,该波的波速为75m/s.
点评:本题是多解问题,关键是会通过波形微平移得到各个质点的振动方向,然后由图象得到周期的通项,最后求解传播速度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示中实线和虚线分别是x轴上沿x轴正方向传播的一列简谐横波在t=0和t=0.03s时刻的波形图,则( )
如图所示中实线和虚线分别是x轴上沿x轴正方向传播的一列简谐横波在t=0和t=0.03s时刻的波形图,则( ) (2006?连云港一模)如图所示,实线和虚线分别表示振幅、频率均相同的两列波的波峰和波谷.此刻,M是波峰与波峰相遇点.下列说法中正确的是( )
(2006?连云港一模)如图所示,实线和虚线分别表示振幅、频率均相同的两列波的波峰和波谷.此刻,M是波峰与波峰相遇点.下列说法中正确的是( )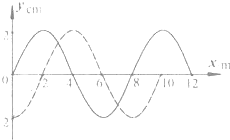 一列简谐横波在x轴上传播,在t1=0和t2=0.05s时刻,其波形图分别用如图所示的实线和虚线表示,求:
一列简谐横波在x轴上传播,在t1=0和t2=0.05s时刻,其波形图分别用如图所示的实线和虚线表示,求: