题目内容
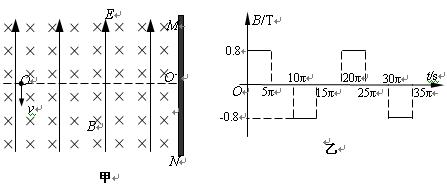
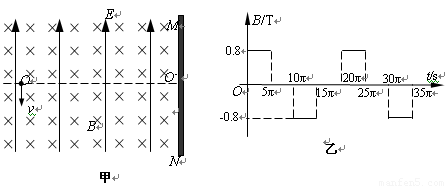
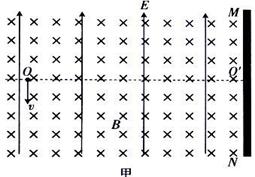
(18分)如图甲所示,竖直挡板MN的左侧空间有方向竖直向上的匀强电场和垂直纸面的水平匀强磁场,电场和磁场的范围足够大,电场强度的大小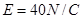 ,磁感应强度B随时间
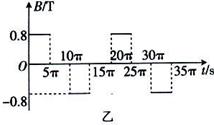
,磁感应强度B随时间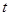 变化的关系图象如图乙所示,选定磁场垂直纸面向里为正方向,在
变化的关系图象如图乙所示,选定磁场垂直纸面向里为正方向,在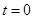 时刻,一质量
时刻,一质量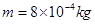 ,带电荷量
,带电荷量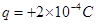 的微粒在O点具有竖直向下的速度
的微粒在O点具有竖直向下的速度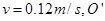 是挡板MN上一点,直线
是挡板MN上一点,直线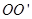 与挡板MN垂直,取
与挡板MN垂直,取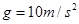 。求:
。求:
⑴微粒下一次经过直线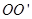 时到O点的距离。
时到O点的距离。
⑵微粒在运动过程中离开直线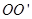 的最大距离。
的最大距离。
⑶水平移动挡板,使微粒能垂直射到挡板上,挡板与O点间距离应满足的条件。
(1)2R="1.2" (m)⑵ ⑶
⑶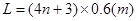 (n=0、1、2、3…..)
(n=0、1、2、3…..)
【解析】
试题分析:(1)由题意知,微粒所受重力:
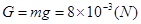 (1分)
(1分)
电场力大小为:  (1分)
(1分)
重力与电场力平衡 ,微粒先在洛伦兹力作用下做匀速圆周运动,则有: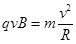 (2分)
(2分)
距O点的距离为:2R="1.2" (m) (2分)
(2)微粒运动半周后向上匀速直线运动,运动时间为:
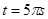 (2分)
(2分)
轨迹如图所示: (2分)
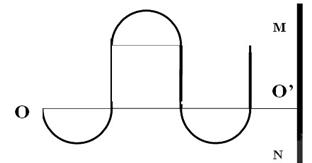
故位移大小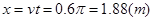 (2分)
(2分)
微粒离开直线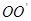 的最大距离:
的最大距离: (2分)
(2分)
(3)若微粒能垂直射到挡板上的某点p,p点在直线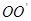 下方时,挡板MN与O点间的距离
下方时,挡板MN与O点间的距离
应满足: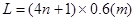 (n=0、1、2、3……) (2分)
(n=0、1、2、3……) (2分)
若微粒能垂直射到挡板上的某点p,p点在直线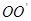 上方时,挡板MN与O点间的距离应满足:
上方时,挡板MN与O点间的距离应满足: (n=1、2、3……)
(2分)
(n=1、2、3……)
(2分)
或 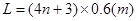 (n=0、1、2、3…..)
(n=0、1、2、3…..)
【若两式合写为: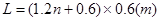 (n=0、1、2、3……)同样给分】
(n=0、1、2、3……)同样给分】
考点:考查带电粒子在复合场中的运动
点评:难度较大,由于粒子运动的往复性造成了多解问题,应首先明确粒子的偏转周期与交变电场的周期关系,以判断那段时间做圆周运动,哪段时间做直线运动

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案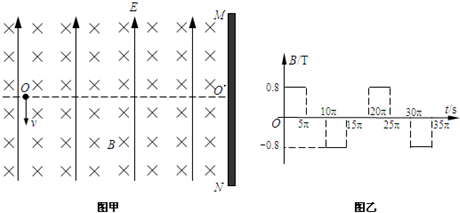
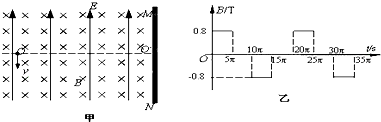 (2013?龙江县二模)如图甲所示,竖直挡板MN左侧空间有方向竖直向上的匀强电场和垂直纸面的水平匀强磁场,电场和磁场的范围足够大,电场强度E=40N/C,磁感应强度B随时间t变化的关系如图乙所示,选定磁场垂直纸面向里为正方向,t=0时刻,一质量m=8×10-4kg、电荷量q=+2×10-4C的微粒在O点具有竖直向下的速度v=0.12m/s,O′是挡板MN上一点,直线OO′与挡板MN垂直,取g=10m/s2,则微粒下一次经过直线OO′时与O点的距离为( )
(2013?龙江县二模)如图甲所示,竖直挡板MN左侧空间有方向竖直向上的匀强电场和垂直纸面的水平匀强磁场,电场和磁场的范围足够大,电场强度E=40N/C,磁感应强度B随时间t变化的关系如图乙所示,选定磁场垂直纸面向里为正方向,t=0时刻,一质量m=8×10-4kg、电荷量q=+2×10-4C的微粒在O点具有竖直向下的速度v=0.12m/s,O′是挡板MN上一点,直线OO′与挡板MN垂直,取g=10m/s2,则微粒下一次经过直线OO′时与O点的距离为( )