题目内容
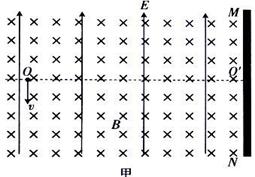
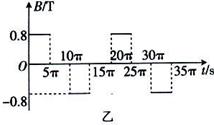
如图甲所示,竖直挡板MN左侧空间有方向竖直向上的匀强电场和垂直纸面向里的水平匀强磁场,电场和磁场的范围足够大,电场强度E=40N/C,磁感应强度B随时间t变化的关系图象如图乙所示,选定磁场垂直纸面向里为正方向.t=0时刻,一质量m=8×10-4kg、电荷量q=+2×10-4C的微粒在O点具有竖直向下的速度v=0.12m/s,O′是挡板MN上一点,直线OO?与挡板MN垂直,取g=10m/s2.求:
(1)微粒再次经过直线OO′时与O点的距离;
(2)微粒在运动过程中离开直线OO′的最大高度;
(3)水平移动挡板,使微粒能垂直到挡板上,挡板与O点间的距离应满足的条件.

(1)微粒再次经过直线OO′时与O点的距离;
(2)微粒在运动过程中离开直线OO′的最大高度;
(3)水平移动挡板,使微粒能垂直到挡板上,挡板与O点间的距离应满足的条件.
分析:(1)微粒所受电场力和重力平衡,知微粒先在磁场中做匀速圆周运动,根据洛伦兹力提供向心力求出轨道半径和周期的大小,确定出在5πs内转过半个圆周,从而求出微粒再次经过直线OO′时与O点的距离.
(2)微粒在5πs内转过半个圆周,然后不受洛伦兹力,向上做匀速直线运动,经过5πs,磁场方向,粒子向右偏转,继续做匀速圆周运动,微粒上的最大高度等于向上做匀速直线运动的位移和圆周运动的半径之和.
(3)讨论微粒打在直线OO?上方和下方,结合图象求出挡板与O点间的距离应满足的条件.
(2)微粒在5πs内转过半个圆周,然后不受洛伦兹力,向上做匀速直线运动,经过5πs,磁场方向,粒子向右偏转,继续做匀速圆周运动,微粒上的最大高度等于向上做匀速直线运动的位移和圆周运动的半径之和.
(3)讨论微粒打在直线OO?上方和下方,结合图象求出挡板与O点间的距离应满足的条件.
解答:解:(1)由题意可知,微粒所受的重力
G=mg=8×10-3N
电场力大小F=Eq=8×10-3N
因此重力与电场力平衡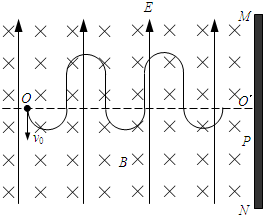
微粒先在洛伦兹力作用下做匀速圆周运动,则qvB=m
解得 R=
=0.6m
由 T=
解得T=10πs
则微粒在5πs内转过半个圆周,再次经直线OO?时与O点的距离
l=2R=1.2m
(2)微粒运动半周后向上匀速运动,运动的时间为t=5πs,轨迹如图所示,位移大小 s=vt=0.6πm=1.88m
因此,微粒离开直线OO?的最大高度
h=s+R=2.48m
(3)若微粒能垂直射到挡板上的某点P,P点在直线OO?下方时,由图象可知,挡板MN与O点间的距离应满足
L=(2.4n+0.6)m(n=0,1,2…)
若微粒能垂直射到挡板上的某点P,P点在直线OO?上方时,由图象可知,挡板MN与O点间的距离应满足 L=(2.4n+1.8)m (n=0,1,2…)
答:(1)微粒再次经过直线OO′时与O点的距离为1.2m.
(2)微粒在运动过程中离开直线OO′的最大高度为2.48m.
(3)若微粒能垂直射到挡板上的某点P,P点在直线OO?下方时,挡板MN与O点间的距离应满足L=(2.4n+0.6)m(n=0,1,2…)
若微粒能垂直射到挡板上的某点P,P点在直线OO?上方时,挡板MN与O点间的距离应满足 L=(2.4n+1.8)m (n=0,1,2…)
G=mg=8×10-3N
电场力大小F=Eq=8×10-3N
因此重力与电场力平衡

微粒先在洛伦兹力作用下做匀速圆周运动,则qvB=m
| v2 |
| R |
解得 R=
| mv |
| Bq |
由 T=
| 2πR |
| v |
解得T=10πs
则微粒在5πs内转过半个圆周,再次经直线OO?时与O点的距离
l=2R=1.2m
(2)微粒运动半周后向上匀速运动,运动的时间为t=5πs,轨迹如图所示,位移大小 s=vt=0.6πm=1.88m
因此,微粒离开直线OO?的最大高度
h=s+R=2.48m
(3)若微粒能垂直射到挡板上的某点P,P点在直线OO?下方时,由图象可知,挡板MN与O点间的距离应满足
L=(2.4n+0.6)m(n=0,1,2…)
若微粒能垂直射到挡板上的某点P,P点在直线OO?上方时,由图象可知,挡板MN与O点间的距离应满足 L=(2.4n+1.8)m (n=0,1,2…)
答:(1)微粒再次经过直线OO′时与O点的距离为1.2m.
(2)微粒在运动过程中离开直线OO′的最大高度为2.48m.
(3)若微粒能垂直射到挡板上的某点P,P点在直线OO?下方时,挡板MN与O点间的距离应满足L=(2.4n+0.6)m(n=0,1,2…)
若微粒能垂直射到挡板上的某点P,P点在直线OO?上方时,挡板MN与O点间的距离应满足 L=(2.4n+1.8)m (n=0,1,2…)
点评:本题是力学与电学综合题,根据匀速圆周运动的规律与几何关系相结合,同时运用力学与电学的知识来解题,从而培养学生分析问题的方法,提升解题的能力.

练习册系列答案
相关题目
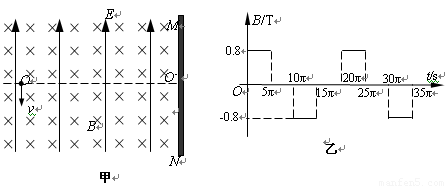
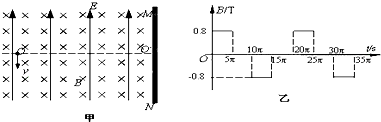 (2013?龙江县二模)如图甲所示,竖直挡板MN左侧空间有方向竖直向上的匀强电场和垂直纸面的水平匀强磁场,电场和磁场的范围足够大,电场强度E=40N/C,磁感应强度B随时间t变化的关系如图乙所示,选定磁场垂直纸面向里为正方向,t=0时刻,一质量m=8×10-4kg、电荷量q=+2×10-4C的微粒在O点具有竖直向下的速度v=0.12m/s,O′是挡板MN上一点,直线OO′与挡板MN垂直,取g=10m/s2,则微粒下一次经过直线OO′时与O点的距离为( )
(2013?龙江县二模)如图甲所示,竖直挡板MN左侧空间有方向竖直向上的匀强电场和垂直纸面的水平匀强磁场,电场和磁场的范围足够大,电场强度E=40N/C,磁感应强度B随时间t变化的关系如图乙所示,选定磁场垂直纸面向里为正方向,t=0时刻,一质量m=8×10-4kg、电荷量q=+2×10-4C的微粒在O点具有竖直向下的速度v=0.12m/s,O′是挡板MN上一点,直线OO′与挡板MN垂直,取g=10m/s2,则微粒下一次经过直线OO′时与O点的距离为( )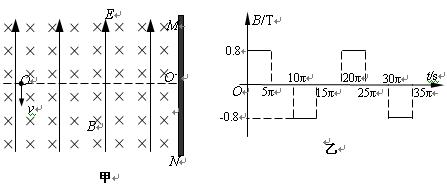
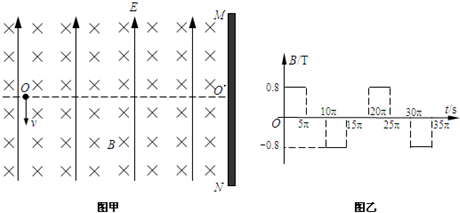
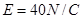 ,磁感应强度B随时间
,磁感应强度B随时间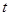 变化的关系图象如图乙所示,选定磁场垂直纸面向里为正方向,在
变化的关系图象如图乙所示,选定磁场垂直纸面向里为正方向,在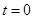 时刻,一质量
时刻,一质量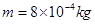 ,带电荷量
,带电荷量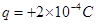 的微粒在O点具有竖直向下的速度
的微粒在O点具有竖直向下的速度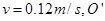 是挡板MN上一点,直线
是挡板MN上一点,直线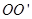 与挡板MN垂直,取
与挡板MN垂直,取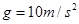 。求:
。求: