题目内容
17. 一光滑的圆锥体固定在水平桌面上,其轴线沿竖直方向,其顶角为60°,如图所示,一条长为L的轻绳,一端固定在锥顶O点,另一端拴一质量为m的小球,小球以速率v0绕圆锥的轴线做水平面内的匀速圆周运动,则以下各项正确的有( )
一光滑的圆锥体固定在水平桌面上,其轴线沿竖直方向,其顶角为60°,如图所示,一条长为L的轻绳,一端固定在锥顶O点,另一端拴一质量为m的小球,小球以速率v0绕圆锥的轴线做水平面内的匀速圆周运动,则以下各项正确的有( )| A. | 当v0=$\sqrt{\frac{\sqrt{3}}{6}}$gL时,小球受三个力作用 | |
| B. | 当vo=$\sqrt{\frac{1}{6}gl}$时,小球受三个力作用 | |
| C. | 当v0=$\sqrt{\frac{3gl}{2}}$时,绳上拉力大小等于2mg | |
| D. | 当v0=$\sqrt{\frac{3gl}{2}}$时,绳与轴线的夹角为60° |
分析 求出物体刚要离开锥面时的速度,此时支持力为零,根据牛顿第二定律求出该临界速度.当速度大于临界速度,则物体离开锥面,当速度小于临界速度,物体还受到支持力,根据牛顿第二定律进行求解.
解答 解: 当物体刚要离开锥面时,支持力为零,根据牛顿第二定律得,$mgtan30°=m\frac{{v}^{2}}{Lsin30°}$,解得临界速度v=$\sqrt{\frac{\sqrt{3}gL}{6}}$,
当物体刚要离开锥面时,支持力为零,根据牛顿第二定律得,$mgtan30°=m\frac{{v}^{2}}{Lsin30°}$,解得临界速度v=$\sqrt{\frac{\sqrt{3}gL}{6}}$,
A、当小球速度${v}_{0}=\sqrt{\frac{\sqrt{3}gL}{6}}$时,小球受两个力作用,故A错误.
B、当${v}_{0}=\sqrt{\frac{1}{6}gL}<v$,知小球未离开锥面,受重力、支持力和拉力作用,故B正确.
C、当${v}_{0}=\sqrt{\frac{3gL}{2}}$>v,知小球离开锥面,小球受重力和拉力两个力作用,$mgtanα=m\frac{{{v}_{0}}^{2}}{Lsinα}$,解得α=60°,
此时绳子的拉力T=$\frac{mg}{cosα}=2mg$,故C正确,D正确.
故选:BCD.
点评 解决本题的关键找出物体的临界情况,以及能够熟练运用牛顿第二定律求解.

练习册系列答案
相关题目
7.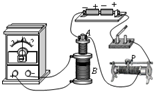 现将电池组、滑动变阻器、带铁芯的线圈A、线圈B、电流计及开关如图连接.在开关闭合、线圈A放在线圈B中的情况下,某同学发现当他将滑线变阻器的滑动端P向左滑动时,电流计指针向右偏转,以下操作也可以使电流计指针向右偏转的是( )
现将电池组、滑动变阻器、带铁芯的线圈A、线圈B、电流计及开关如图连接.在开关闭合、线圈A放在线圈B中的情况下,某同学发现当他将滑线变阻器的滑动端P向左滑动时,电流计指针向右偏转,以下操作也可以使电流计指针向右偏转的是( )
 现将电池组、滑动变阻器、带铁芯的线圈A、线圈B、电流计及开关如图连接.在开关闭合、线圈A放在线圈B中的情况下,某同学发现当他将滑线变阻器的滑动端P向左滑动时,电流计指针向右偏转,以下操作也可以使电流计指针向右偏转的是( )
现将电池组、滑动变阻器、带铁芯的线圈A、线圈B、电流计及开关如图连接.在开关闭合、线圈A放在线圈B中的情况下,某同学发现当他将滑线变阻器的滑动端P向左滑动时,电流计指针向右偏转,以下操作也可以使电流计指针向右偏转的是( )| A. | 断开开关的瞬间 | |
| B. | 闭合开关的瞬间 | |
| C. | 在开关闭合的情况下,向上移动线圈A的过程中 | |
| D. | 在开关闭合的情况下,滑动变阻器的滑动端P向右滑动的过程中 |
8.一矿井深125m,在井口每隔一定时间自由下落一个小球,当第11个小球刚从井口开始下落时,第1个小球恰好到达井底,则下列关于小球运动的说法正确的是(g取10m/s2)( )
| A. | 相邻两个小球间的时间间隔为0.5 s | |
| B. | 相邻两个小球间的时间间隔为1 s | |
| C. | 第3个小球和第5个小球间的距离为35 m | |
| D. | 第3个小球和第5个小球间的距离为25 m |
12.在光滑水平面上,动能为E0、动量的大小为P0的小钢球1与静止小钢球2发生碰撞,碰撞前后球1的运动方向相反.将碰撞后球1的动能和动量的大小分别记为E1、P1,球2的动能和动量的大小分别记为E2、P2,则不可能有( )
| A. | E1<E0 | B. | p1<p0 | C. | E2>E0 | D. | p2>p0 |
2.由于放射性元素${\;}_{93}^{237}$Np的半衰期很短,所以在自然界一直未被发现,只是在使用人工的方法制造后才被发现.已知${\;}_{93}^{237}$Np经过一系列α衰变和β衰变后变成${\;}_{83}^{209}$Bi,下列判断中正确的是( )
| A. | ${\;}_{83}^{209}$Bi的原子核比${\;}_{93}^{237}$Np的原子核少28个中子 | |
| B. | ${\;}_{83}^{209}$Bi的原子核比${\;}_{93}^{237}$Np的原子核少18个中子 | |
| C. | 衰变过程中共发生了7次α衰变和4次β衰变 | |
| D. | 衰变过程中共发生了4次α衰变和7次β衰变 | |
| E. | 降低元素${\;}_{93}^{237}$Np周围环境温度不能延长其半衰期 |
9.关于力和运动的关系,下列说法中正确的是( )
| A. | 力是产生位移的原因 | B. | 力是维持物体运动的原因 | ||
| C. | 力是改变物体速度的原因 | D. | 力是物体获得速度的原因 |

 如图所示,把A、B两个完全相同的小球分别用长度均为l=0.10m的绝缘细线连接,悬挂于O点,使小球带上等量正电荷.A、B小球平衡时距离为d=0.12m.已测得每个小球质量是1.2×10-3kg,带电小球可视为点电荷,重力加速度g=10m/s2,静电力常量K=9.0×109 N•m2/C2
如图所示,把A、B两个完全相同的小球分别用长度均为l=0.10m的绝缘细线连接,悬挂于O点,使小球带上等量正电荷.A、B小球平衡时距离为d=0.12m.已测得每个小球质量是1.2×10-3kg,带电小球可视为点电荷,重力加速度g=10m/s2,静电力常量K=9.0×109 N•m2/C2