题目内容
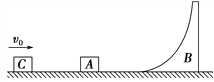
【题目】如图所示,光滑水平面上依次放置两个质量均为m的小物块A和C以及光滑曲面劈B,B的质量为M=3m,劈B的曲面下端与水平面相切,且劈B足够高。现让小物块C以水平速度v0向右运动,与A发生弹性碰撞,碰撞后小物块A又滑上劈B。求物块A在B上能够达到的最大高度。
【答案】![]()
【解析】试题分析:选取A、C系统碰撞过程动量守恒,机械能守恒,应用动量守恒定律与机械能守恒定律求出A的速度;A、B系统在水平方向动量守恒,由动量守恒定律与机械能守恒定律可以解题。
小物块C与A发生弹性碰撞,
由动量守恒得:mv0=mvC+mvA
由机械能守恒定律得:![]()
联立以上解得:vC=0,vA=v0
设小物块A在劈B上达到的最大高度为h,此时小物块A和B的共同速度大小为
v,对小物块A与B组成的系统,
由机械能守恒得:![]()
水平方向动量守恒![]()
联立以上解得: ![]()

练习册系列答案
相关题目