Question

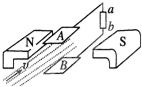
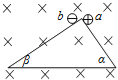
【题目】如图所示，足够长的光滑三角形绝缘槽，与水平面的夹角分别为α和β（α＜β），加垂直于纸面向里的磁场．分别将质量相等、带等量正、负电荷的小球 a、b依次从两斜面的顶端由静止释放，关于两球在槽上运动的说法正确的是（ ）

A. 在槽上，a、b两球都做匀加速直线运动，且aa＞ab

B. a、b两球沿槽运动的最大速度为va和vb，则va＞vb

C. a、b两球沿直槽运动的最大位移为Sa和Sb，则Sa＜Sb

D. a、b两球沿槽运动的时间为ta和tb，则ta＜tb

Answer 1

【答案】ACD

【解析】试题分析：对两球分别进行受力分析，确定合力后，再由牛顿第二定律可以求出加速度，然后比较加速度大小，判断小球的运动性质；求出小球在斜面上运动的位移与运动时间，然后答题．

解：A、两小球受到的洛伦兹力都与斜面垂直向上，沿斜面方向的合力为重力的分力，则其加速度为aa=gsinα ab=gsinβ

可见aa＞ab故A正确；

B、当加速到洛伦兹力与重力沿垂直斜面向下分力相等时，小球脱离斜面

则 mgcosβ=Bqv

所以：，

由于（α＞β）所以va＜vb，故B错误；

C、又 V2=2gsinαsa 求得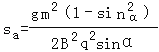

同理得：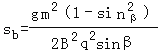

因α＞β，则 sa＜sb故C正确，

D、又由v=gsinβta得

同理得

则ta＜tb则D正确

故选：ACD