题目内容
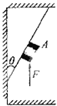在建筑装修中，工人用质量为m=5.0kg的磨石A对倾角θ=370的斜壁进行打磨，A与斜壁之间的动摩擦因数μ=0.5，如图所示，当对A加竖直向上推力F=60N时，则磨石A从静止开始沿斜壁向上运动2m（斜壁长＞2m）所需时间为多少？（g取10m/s2，sin37°=0.6，cos37°=0.8）分析：对A受力分析，根据牛顿第二定律求出加速度的大小，再通过运动学公式求出运动的时间．
解答：解：A的受力如图，根据牛顿第二定律得，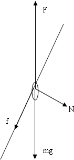
a=
=1m/s2．
根据x=
at2得，t=
=2s
答：磨石A从静止开始沿斜壁向上运动2m所需的时间为2s．
a=| (F-mg)cos37°-μ(F-mg)sin37° |
| m |
根据x=
| 1 |
| 2 |
|
答：磨石A从静止开始沿斜壁向上运动2m所需的时间为2s．
点评：解决本题的关键知道加速度是联系力学和运动学的桥梁，通过加速度可以根据力求运动，也可以根据运动求力．
练习册系列答案
名校课堂系列答案
相关题目
如图所示，在建筑装修中，工人用质量为5.0kg的磨石A对地面和斜壁进行打磨，已知A与地面、A与斜壁之间的动摩擦因数μ均相同．（g取10m/s2 且sin37°=0.6，cos37°=0.8）
（2012?聊城模拟）在建筑装修中，工人用质量为M的磨石对斜壁进行打磨，当对磨石加竖直向上推力F时，磨石恰好沿斜壁向上匀速运动，已知磨石与斜壁之间的动摩擦因素为μ，则磨石受到的摩擦力是（ ）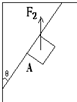
在建筑装修中，工人用质量为5kg的磨石A对地面和斜壁进行打磨，已知磨石A与地面和斜壁之间的动摩擦因数?均相同．
在建筑装修中，工人用质量为m的磨石对斜壁（斜壁与竖直方向的夹角为θ）进行打磨，如图所示．当对磨石加竖直向上的推力F时，磨石恰好沿斜壁匀速向上运动．已知磨石与斜壁之间的动摩擦因数为μ，则磨石受到的摩擦力是（ ）| A、（mg-F）sinθ | B、μ（mg-F）sinθ | C、μ（F-mg）sinθ | D、（F-mg）cosθ |