题目内容
【题目】竖直平面内有两个半径不同的半圆形光滑轨道，如图所示，A、M、B三点位于同一水平面上，C、D分别为两轨道的最低点，将两个相同的小球分别从A、B处同时无初速释放，则下列说法中不正确的是（ ）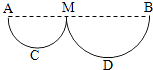
A.通过C，D时，两球的加速度相等
B.通过C，D时，两球的机械能相等
C.通过C，D时，两球对轨道的压力相等
D.通过C，D时，两球的速度大小相等
【答案】D
【解析】解：A、对任意一球，设通过最低点时的速度大小为v．轨道半径为r．由机械能守恒得 mgr= 
，得 v= 
，通过最低点的加速度 a= 
= 
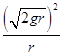=2g，与轨道半径无关，所以通过C、D时，两球的加速度相等，故A正确．
B、选择相同的参考平面，在初始位置时两球的机械能相同，下滑过程只有重力做功，机械能都守恒，所以通过C、D时，两球的机械能相等，故B正确．
C、在最低点，有 N﹣mg=ma，可得 N=3mg，由牛顿第三定律知，小球对轨道的压力大小也为3mg，与轨道半径无关，所以两球通过最低点时对轨道的压力相等，故C正确．
D、由v= ，知通过C、D时，两球的速度大小不等，故D错误．
本题选不正确的，故选：D
【考点精析】关于本题考查的向心力和机械能守恒及其条件，需要了解向心力总是指向圆心，产生向心加速度，向心力只改变线速度的方向，不改变速度的大小；向心力是根据力的效果命名的.在分析做圆周运动的质点受力情况时，千万不可在物体受力之外再添加一个向心力；在只有重力（和弹簧弹力）做功的情形下，物体动能和重力势能（及弹性势能）发生相互转化，但机械能的总量保持不变才能得出正确答案．
练习册系列答案
相关题目
