题目内容
 如图所示.在同一竖直平面内,一轻质弹簧静止放于光滑斜面上,其一端固定,另一端恰好与水平线AB平齐;长为L的轻质细线一端固定在O点,另一端系一质量为m的小球,将细线拉至水平,此时小球在位置C.现由静止释放小球,小球到达最低点D时,细线恰好被拉断,D点与AB相距h;之后小球在运动过程中恰好与弹簧接触并沿斜面方向压缩弹簧,弹簧最大压缩量为x.试求:
如图所示.在同一竖直平面内,一轻质弹簧静止放于光滑斜面上,其一端固定,另一端恰好与水平线AB平齐;长为L的轻质细线一端固定在O点,另一端系一质量为m的小球,将细线拉至水平,此时小球在位置C.现由静止释放小球,小球到达最低点D时,细线恰好被拉断,D点与AB相距h;之后小球在运动过程中恰好与弹簧接触并沿斜面方向压缩弹簧,弹簧最大压缩量为x.试求:(1)斜面的倾角θ
(2)弹簧所获得的最大的弹性势能EP.
分析:(1)C到D过程,小球的机械能守恒,可求出小球到D点时的速度.细绳在D点被拉断后小球做平抛运动,由题意,小球在运动过程中恰好沿斜面方向将弹簧压缩,速度沿斜面向下方向.由平抛运动知识求出小球到达D时竖直方向的分速度,由tanθ=
求出斜面的倾角.
(2)当弹簧的压缩量最大时弹簧所获得的最大弹性势能,根据系统的机械能守恒求解.
| vy |
| vD |
(2)当弹簧的压缩量最大时弹簧所获得的最大弹性势能,根据系统的机械能守恒求解.
解答:解:( 1)小球从C到D,机械能守恒,则得:mgL=
?mvD2
得vD=
绳断后,小球从D到A做平抛运动:h=
gt2,得t=
竖直分速度 vy=
斜面的倾角θ有:tanθ=
=
所以θ=arctan
(2)小球从C经D,A到弹簧压缩最大间,小球与弹簧的总机械能守恒,小球减少的重力势能全转化为弹簧所储存的弹性势能EP=mg(L+h+xsinθ)
其中sinθ=
所以 EP=mg(x
+h+L)
答:
(1)斜面的倾角θ为arctan
.
(2)弹簧所获得的最大的弹性势能EP是mg(x
+h+L).
| 1 |
| 2 |
得vD=
| 2gL |
绳断后,小球从D到A做平抛运动:h=
| 1 |
| 2 |
|
竖直分速度 vy=
| 2gh |
斜面的倾角θ有:tanθ=
| vy |
| vD |
|
|
(2)小球从C经D,A到弹簧压缩最大间,小球与弹簧的总机械能守恒,小球减少的重力势能全转化为弹簧所储存的弹性势能EP=mg(L+h+xsinθ)
其中sinθ=
|
所以 EP=mg(x
|
答:
(1)斜面的倾角θ为arctan
|
(2)弹簧所获得的最大的弹性势能EP是mg(x
|
点评:本题是圆周运动、平抛运动、机械能守恒的综合,情景简单,应按程序进行分析和求解.

练习册系列答案
相关题目
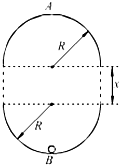 如图所示,在同一竖直平面内有两个正对着的半圆形光滑轨道,轨道的半径都是R.轨道端点所在的水平线相隔一定的距离x.一质量为m的小球能在其间运动而不脱离轨道,经过最低点B时的速度为v.小球在最低点B与最高点A对轨道的压力之差为△F(△F>0),不计空气阻力.则( )
如图所示,在同一竖直平面内有两个正对着的半圆形光滑轨道,轨道的半径都是R.轨道端点所在的水平线相隔一定的距离x.一质量为m的小球能在其间运动而不脱离轨道,经过最低点B时的速度为v.小球在最低点B与最高点A对轨道的压力之差为△F(△F>0),不计空气阻力.则( )| A、m、x一定时,R越大,△F一定越大 | B、m、R一定时,x越大,△F一定越大 | C、m、x一定时,v越大,△F一定越大 | D、m、R一定时,v越大,△F一定越大 |
 质量4㎏的物体放在水平地面上,在一大小30N的水平外力作用下,恰能沿水平方向做匀速运动.求:
质量4㎏的物体放在水平地面上,在一大小30N的水平外力作用下,恰能沿水平方向做匀速运动.求: (2007?广东)如图所示,在同一竖直面上,质量为2m的小球A静止在光滑斜面的底部,斜面高度为H=2L.小球受到弹簧的弹性力作用后,沿斜面向上运动.离开斜面后,达到最高点时与静止悬挂在此处的小球B发生弹性碰撞,碰撞后球B刚好能摆到与悬点O同一高度,球A沿水平方向抛射落在水平面C上的P点,O点的投影O′与P的距离为L/2.已知球B质量为m,悬绳长L,视两球为质点,重力加速度为g,不计空气阻力,求:
(2007?广东)如图所示,在同一竖直面上,质量为2m的小球A静止在光滑斜面的底部,斜面高度为H=2L.小球受到弹簧的弹性力作用后,沿斜面向上运动.离开斜面后,达到最高点时与静止悬挂在此处的小球B发生弹性碰撞,碰撞后球B刚好能摆到与悬点O同一高度,球A沿水平方向抛射落在水平面C上的P点,O点的投影O′与P的距离为L/2.已知球B质量为m,悬绳长L,视两球为质点,重力加速度为g,不计空气阻力,求: 如图所示,在同一竖直平面内两正对着的半径为R的相同半圆光滑轨道,相隔一定的距离x,虚线沿竖直方向,一质量为m的小球能在其间运动.今在最低点B与最高点A各放一个压力传感器,测试小球对轨道的压力,并通过计算机显示出来.(不计空气阻力,g取10m/s2)
如图所示,在同一竖直平面内两正对着的半径为R的相同半圆光滑轨道,相隔一定的距离x,虚线沿竖直方向,一质量为m的小球能在其间运动.今在最低点B与最高点A各放一个压力传感器,测试小球对轨道的压力,并通过计算机显示出来.(不计空气阻力,g取10m/s2)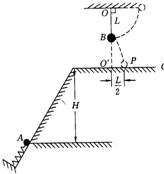 如图所示,在同一竖直平面上,质量为2m的小球A静止在光滑斜面的底部,斜面高度为H=2L,小球受到弹簧的弹性力作用后,沿斜面向上运动.离开斜面后,达到最高点时与静止悬挂在此处的小球B发生碰撞,碰撞中无机械能损失,碰撞后球B刚好能摆到与悬点O同一高度,球A沿水平方向抛射落在水平面C上的P点,O点的投影O'与P点的距离为L/2.已知球B质量为m,悬绳长L,视两球为质点,重力加速度为g,不计空气阻力,求:
如图所示,在同一竖直平面上,质量为2m的小球A静止在光滑斜面的底部,斜面高度为H=2L,小球受到弹簧的弹性力作用后,沿斜面向上运动.离开斜面后,达到最高点时与静止悬挂在此处的小球B发生碰撞,碰撞中无机械能损失,碰撞后球B刚好能摆到与悬点O同一高度,球A沿水平方向抛射落在水平面C上的P点,O点的投影O'与P点的距离为L/2.已知球B质量为m,悬绳长L,视两球为质点,重力加速度为g,不计空气阻力,求: