题目内容
16.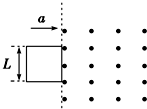 如图所示,虚线右侧存在匀强磁场,磁场方向垂直纸面向外,正方形金属框电阻为R,边长为L,自线框从左边界进入磁场时开始计时,在外力作用下由静止开始,以垂直于磁场边界的恒定加速度a进入磁场区域,t1时刻线框全部进入磁场.规定顺时针方向为感应电流i的正方向.外力大小为F,线框中电功率的瞬时值为P,通过导体横截面的电荷量为q,则这些量随时间变化的关系正确的是( )
如图所示,虚线右侧存在匀强磁场,磁场方向垂直纸面向外,正方形金属框电阻为R,边长为L,自线框从左边界进入磁场时开始计时,在外力作用下由静止开始,以垂直于磁场边界的恒定加速度a进入磁场区域,t1时刻线框全部进入磁场.规定顺时针方向为感应电流i的正方向.外力大小为F,线框中电功率的瞬时值为P,通过导体横截面的电荷量为q,则这些量随时间变化的关系正确的是( )| A. | 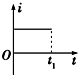 | B. | 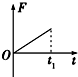 | C. | 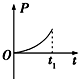 | D. | 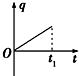 |
分析 由线框进入磁场中切割磁感线,根据运动学公式可知速度与时间关系;由法拉第电磁感应定律E=BLv,可得出产生感应电动势与速度关系,由闭合电路欧姆定律来确定感应电流的大小,并由安培力公式可确定其大小与时间的关系;由牛顿第二定律来确定合力与时间的关系;最后电量、功率的表达式来分别得出各自与时间的关系.
解答 解:A、线框做匀加速运动,其速度v=at,感应电动势E=BLv,感应电流 i=$\frac{E}{R}$=$\frac{BLat}{R}$,i与t成正比,故A错误.
B、线框进入磁场过程中受到的安培力FB=BiL=$\frac{{B}^{2}{L}^{2}at}{R}$,由牛顿第二定律得:F-FB=ma,得 F=ma+$\frac{{B}^{2}{L}^{2}at}{R}$,F-t图象是不过原点的倾斜直线,故B错误.
C、线框的电功率 P=i2R=$\frac{(BLat)^{2}}{R}$∝t2,故C正确.
D、线框的位移x=$\frac{1}{2}$at2,电荷量q=$\overline{I}$△t=$\frac{\overline{E}}{R}$△t=$\frac{△Φ}{R}$=$\frac{BLx}{R}$=$\frac{BL•\frac{1}{2}a{t}^{2}}{R}$∝t2,q-t图象应是抛物线.故D错误;
故选:C.
点评 解决本题的关键掌握运动学公式,并由各自表达式来进行推导,从而得出结论是否正确,以及掌握切割产生的感应电动势E=BLv.知道L为有效长度.

练习册系列答案
相关题目
6.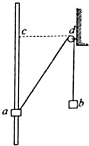 如图所示,固定的粗糙竖直杆上套有小物块a,不可伸长的轻质细绳通过大小可忽略的定滑轮连接物块a和小物块b,虚线cd水平.现由静止释放两物块,物块a从图示位置上升,并恰好能到达c处.在此过程中,若不计绳和定滑轮之间的摩擦和空气阻力,下列说法正确的是( )
如图所示,固定的粗糙竖直杆上套有小物块a,不可伸长的轻质细绳通过大小可忽略的定滑轮连接物块a和小物块b,虚线cd水平.现由静止释放两物块,物块a从图示位置上升,并恰好能到达c处.在此过程中,若不计绳和定滑轮之间的摩擦和空气阻力,下列说法正确的是( )
 如图所示,固定的粗糙竖直杆上套有小物块a,不可伸长的轻质细绳通过大小可忽略的定滑轮连接物块a和小物块b,虚线cd水平.现由静止释放两物块,物块a从图示位置上升,并恰好能到达c处.在此过程中,若不计绳和定滑轮之间的摩擦和空气阻力,下列说法正确的是( )
如图所示,固定的粗糙竖直杆上套有小物块a,不可伸长的轻质细绳通过大小可忽略的定滑轮连接物块a和小物块b,虚线cd水平.现由静止释放两物块,物块a从图示位置上升,并恰好能到达c处.在此过程中,若不计绳和定滑轮之间的摩擦和空气阻力,下列说法正确的是( )| A. | 物块a到达c点时加速度为零 | |
| B. | 绳拉力对物块a做的功等于物块a重力势能的增加量 | |
| C. | 绳拉力对物块a始终做正功 | |
| D. | 摩擦力对a做的功等于物块a、b系统机械能的变化量 |
7.如图所示,空间有一电场,电场中有两个点a和b.下列说法正确的是( )


| A. | 该电场是匀强电场 | |
| B. | a点的电场强度比b点的大 | |
| C. | b点的电场强度比a点的大 | |
| D. | 正电荷在a、b两点受电场力方向相同 |
1.2015年2月7日,木星发生“冲日”现象,“木星冲日”是指木星和太阳正好分处地球的两侧,三者成一条直线,木星和地球绕太阳公转的方向相同,公转轨迹都近似为圆,设木星公转半径为R1,周期为T1;地球公转半径为R2,周期为T2.下列说法正确的是( )
| A. | $\frac{T_1}{T_2}={({\frac{R_1}{R_2}})^{\frac{2}{3}}}$ | |
| B. | $\frac{T_1}{T_2}={({\frac{R_1}{R_2}})^{\frac{3}{2}}}$ | |
| C. | “木星冲日”这一天象的发生周期为$\frac{{2{T_1}{T_2}}}{{{T_1}-{T_2}}}$ | |
| D. | “木星冲日”这一天象的发生周期为$\frac{{{T_1}{T_2}}}{{{T_1}-{T_2}}}$ |
8. 如图所示,同种介质中有两列简谐横波相向传播,实线表示的波沿x轴正方向传播,虚线表示的波沿x轴负方向传播,在t=0时刻,两列波已在0≤x≤2m范围内相遇.已知波的频率为5Hz.两列波的振幅均为2cm,则下列说法正确的是( )
如图所示,同种介质中有两列简谐横波相向传播,实线表示的波沿x轴正方向传播,虚线表示的波沿x轴负方向传播,在t=0时刻,两列波已在0≤x≤2m范围内相遇.已知波的频率为5Hz.两列波的振幅均为2cm,则下列说法正确的是( )
 如图所示,同种介质中有两列简谐横波相向传播,实线表示的波沿x轴正方向传播,虚线表示的波沿x轴负方向传播,在t=0时刻,两列波已在0≤x≤2m范围内相遇.已知波的频率为5Hz.两列波的振幅均为2cm,则下列说法正确的是( )
如图所示,同种介质中有两列简谐横波相向传播,实线表示的波沿x轴正方向传播,虚线表示的波沿x轴负方向传播,在t=0时刻,两列波已在0≤x≤2m范围内相遇.已知波的频率为5Hz.两列波的振幅均为2cm,则下列说法正确的是( )| A. | 波的传播速度为40m/s | |
| B. | 在t=0时刻,x=4处的质点向上运动 | |
| C. | 两列波相遇后,x=1m处质点的振幅为4cm | |
| D. | 在t=0.1s时刻,x=-4m处的质点运动到x=0处 |
5.下列不属于电磁波的是( )
| A. | 红外线 | B. | X射线 | C. | β射线 | D. | γ射线 |
6.超市货架陈列着四个完全相同的篮球,不计摩擦,挡板均竖直,则4球中对圆弧面压力最小的球是( )

| A. | a球 | B. | b球 | C. | c球 | D. | d球 |
 光滑水平地面上,人与滑板A一起以v0=0.5m/s的速度前进,正前方不远处有一横杆,横杆另一侧有一静止滑板B,当人与A行至横杆前,人相对滑板竖直向上起跳越过横杆,A从横杆下方通过并与B发生弹性碰撞,之后人刚好落到B上,不计空气阻力,求最终人与B共同速度是多少?已知m人=40kg,mA=5kg,mB=10kg.
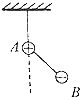
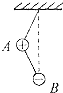
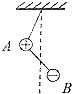
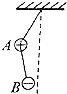
光滑水平地面上,人与滑板A一起以v0=0.5m/s的速度前进,正前方不远处有一横杆,横杆另一侧有一静止滑板B,当人与A行至横杆前,人相对滑板竖直向上起跳越过横杆,A从横杆下方通过并与B发生弹性碰撞,之后人刚好落到B上,不计空气阻力,求最终人与B共同速度是多少?已知m人=40kg,mA=5kg,mB=10kg.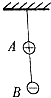 如图所示,A、B两带电小球的质量分布为2m,m,所带电量分布为3q和-q,两球间用绝缘细线相连,A球又用等长的绝缘细线悬挂在天花板上(两球的大小可忽略不计),在两球所在空间有水平向左的匀强电场,电场强度为E,平衡时细线都被拉紧,平衡时的可能位置是图中的( )
如图所示,A、B两带电小球的质量分布为2m,m,所带电量分布为3q和-q,两球间用绝缘细线相连,A球又用等长的绝缘细线悬挂在天花板上(两球的大小可忽略不计),在两球所在空间有水平向左的匀强电场,电场强度为E,平衡时细线都被拉紧,平衡时的可能位置是图中的( )