题目内容
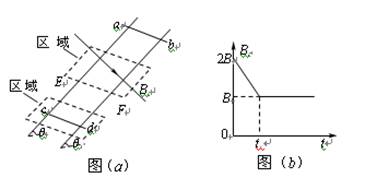
 如图(a)所示,间距为l、电阻不计的光滑导轨固定在倾角为θ的斜面上.在区域I内有方向垂直于斜面的匀强磁场,磁感应强度为B;在区域Ⅱ内有垂直于斜面向下区域I区域Ⅱ有垂直于斜面向下的匀强磁场,其磁感应强度Bt的大小随时间t变化的规律如图(b)所示.t=0时刻在轨道上端的金属细棒ab从如图位置由静止开始沿导轨下滑,同时下端的另一金属细棒cd在位于区域I内的导轨上由静止释放.在ab棒运动到区域Ⅱ的下边界EF处之前,cd棒始终静止不动,两棒均与导轨接触良好.
如图(a)所示,间距为l、电阻不计的光滑导轨固定在倾角为θ的斜面上.在区域I内有方向垂直于斜面的匀强磁场,磁感应强度为B;在区域Ⅱ内有垂直于斜面向下区域I区域Ⅱ有垂直于斜面向下的匀强磁场,其磁感应强度Bt的大小随时间t变化的规律如图(b)所示.t=0时刻在轨道上端的金属细棒ab从如图位置由静止开始沿导轨下滑,同时下端的另一金属细棒cd在位于区域I内的导轨上由静止释放.在ab棒运动到区域Ⅱ的下边界EF处之前,cd棒始终静止不动,两棒均与导轨接触良好.已知cd棒的质量为m、电阻为R,ab棒的质量、阻值均未知,区域Ⅱ沿斜面的长度为2l,在t=tx时刻(tx未知)ab棒恰进入区域Ⅱ,重力加速度为g.求:
(1)通过cd棒电流的方向和区域I内磁场的方向;
(2)当ab棒在区域Ⅱ内运动时cd棒消耗的电功率;
(3)ab棒开始下滑的位置离EF的距离;
(4)ab棒开始下滑至EF的过程中回路中产生的热量.
分析:(1)根据右手定则判断出ab棒中的电流方向,从而得出通过cd棒中的电流方向,根据cd棒处于静止,通过安培力的方向,根据左手定则判断出区域I内磁场的方向.
(2)对cd棒,根据平衡求出感应电流的大小,根据P=I2R求出当ab棒在区域II内运动时cd棒消耗的电功率.
(3)棒ab进入II区域前后回路中的电动势不变,即磁场变化产生电动势与导体切割磁感线产生电动势相等,据此求出导体棒进入II时速度大小,然后根据导体棒匀加速下滑的特点即可求出结果.
(4)回路中电流恒定,根据Q=EIt可求出结果.
(2)对cd棒,根据平衡求出感应电流的大小,根据P=I2R求出当ab棒在区域II内运动时cd棒消耗的电功率.
(3)棒ab进入II区域前后回路中的电动势不变,即磁场变化产生电动势与导体切割磁感线产生电动势相等,据此求出导体棒进入II时速度大小,然后根据导体棒匀加速下滑的特点即可求出结果.
(4)回路中电流恒定,根据Q=EIt可求出结果.
解答:解:(1)通过cd棒的电流方向 d→c
区域I内磁场方向为垂直于斜面向上
(2)对cd棒,F安=BIl=mgsinθ所以通过cd棒的电流大小I=
当ab棒在区域II内运动时cd棒消耗的电功率P=I2R=
.
(3)ab棒在到达区域II前做匀加速直线运动,a=
=gsinθ
cd棒始终静止不动,ab棒在到达区域II前、后,回路中产生的感应电动势不变,则ab棒在区域II中一定做匀速直线运动
可得;
=Blvt
=Blgsinθt x 所以t x=
ab棒在区域II中做匀速直线运动的速度vt=
则ab棒开始下滑的位置离EF的距离h=
a t x2+2l=3 l
(4)ab棒在区域II中运动的时间t2=
=
ab棒从开始下滑至EF的总时间t=t x+t2=2
ε=Blvt=Bl
ab棒从开始下滑至EF的过程中闭合回路中产生的热量:Q=εIt=4mglsinθ
答:(1)通过cd棒的电流方向 d→c,区域I内磁场方向为垂直于斜面向上.
(2)当ab棒在区域Ⅱ内运动时cd棒消耗的电功率为
.
(3)ab棒开始下滑的位置离EF的距离为3l.
(4)ab棒开始下滑至EF的过程中回路中产生的热量为Bl
.
区域I内磁场方向为垂直于斜面向上
(2)对cd棒,F安=BIl=mgsinθ所以通过cd棒的电流大小I=
| mgsinθ |
| Bl |
当ab棒在区域II内运动时cd棒消耗的电功率P=I2R=
| m2g2Rsin2θ |
| B2l2 |
(3)ab棒在到达区域II前做匀加速直线运动,a=
| F合 |
| m |
cd棒始终静止不动,ab棒在到达区域II前、后,回路中产生的感应电动势不变,则ab棒在区域II中一定做匀速直线运动
可得;
| △φ |
| △t |
| B?2l?l |
| tx |
|
ab棒在区域II中做匀速直线运动的速度vt=
| 2glsinθ |
则ab棒开始下滑的位置离EF的距离h=
| 1 |
| 2 |
(4)ab棒在区域II中运动的时间t2=
| 2l |
| vt |
|
ab棒从开始下滑至EF的总时间t=t x+t2=2
|
ε=Blvt=Bl
| 2glsinθ |
ab棒从开始下滑至EF的过程中闭合回路中产生的热量:Q=εIt=4mglsinθ
答:(1)通过cd棒的电流方向 d→c,区域I内磁场方向为垂直于斜面向上.
(2)当ab棒在区域Ⅱ内运动时cd棒消耗的电功率为
| m2g2Rsin2θ |
| B2l2 |
(3)ab棒开始下滑的位置离EF的距离为3l.
(4)ab棒开始下滑至EF的过程中回路中产生的热量为Bl
| 2glsinθ |
点评:解决这类问题的关键是弄清电路结构,正确分析电路中的电流以及安培力的变化情况.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
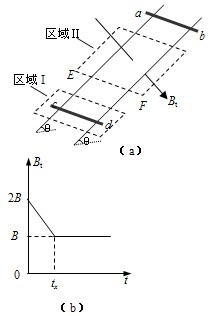
 如图(a)所示,间距为L、电阻不计的光滑导轨固定在倾角为θ的斜面上.在区域I内有方向垂直于斜面向上的匀强磁场,磁感应强度为B;在区域Ⅱ内有垂直于斜面向下的匀强磁场,其磁感应强度Bt的大小随时间t变化的规律如下图(b)所示.t=0时刻在轨道上端的金属细棒ab从如图位置由静止开始沿导轨下滑,同时下端的另一金属细棒cd在位于区域I内的导轨上由静止释放.在ab棒运动到区域Ⅱ的下边界EF处之前,cd棒始终静止不动,两棒均与导轨接触良好.已知cd棒的质量为m、电阻为R,ab棒的质量未知、阻值为r,区域Ⅱ沿斜面的长度为2L,在t=tx时刻(tx未知)ab棒恰好进入区域Ⅱ,重力加速度为g.求:
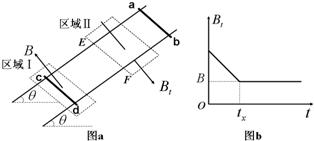
如图(a)所示,间距为L、电阻不计的光滑导轨固定在倾角为θ的斜面上.在区域I内有方向垂直于斜面向上的匀强磁场,磁感应强度为B;在区域Ⅱ内有垂直于斜面向下的匀强磁场,其磁感应强度Bt的大小随时间t变化的规律如下图(b)所示.t=0时刻在轨道上端的金属细棒ab从如图位置由静止开始沿导轨下滑,同时下端的另一金属细棒cd在位于区域I内的导轨上由静止释放.在ab棒运动到区域Ⅱ的下边界EF处之前,cd棒始终静止不动,两棒均与导轨接触良好.已知cd棒的质量为m、电阻为R,ab棒的质量未知、阻值为r,区域Ⅱ沿斜面的长度为2L,在t=tx时刻(tx未知)ab棒恰好进入区域Ⅱ,重力加速度为g.求: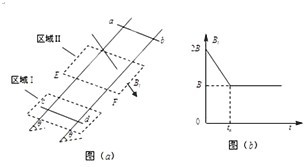 如图(a)所示,间距为L电阻不计的光滑导轨固定在倾角为θ的斜面上.在区域I内有方向垂直于斜面的匀强磁场,磁感应强度恒为B不变;在区域Ⅱ内有垂直于斜面向下的匀强磁场,其磁感应强度Bt的大小随时间t变化的规律如图(b)所示.t=0时刻在轨道上端的金属细棒ab从如图位置由静止开始沿导轨下滑,同时下端的另一金属细棒cd在位于区域I内的导轨上也由静止释放.在ab棒运动到区域Ⅱ的下边界EF之前,cd棒始终静止不动,两棒均与导轨接触良好.又已知cd棒的质量为m,区域Ⅱ沿斜面的长度也是L,在t=tx时刻(tx未知)ab棒恰好进入区域Ⅱ,重力加速度为g.求:
如图(a)所示,间距为L电阻不计的光滑导轨固定在倾角为θ的斜面上.在区域I内有方向垂直于斜面的匀强磁场,磁感应强度恒为B不变;在区域Ⅱ内有垂直于斜面向下的匀强磁场,其磁感应强度Bt的大小随时间t变化的规律如图(b)所示.t=0时刻在轨道上端的金属细棒ab从如图位置由静止开始沿导轨下滑,同时下端的另一金属细棒cd在位于区域I内的导轨上也由静止释放.在ab棒运动到区域Ⅱ的下边界EF之前,cd棒始终静止不动,两棒均与导轨接触良好.又已知cd棒的质量为m,区域Ⅱ沿斜面的长度也是L,在t=tx时刻(tx未知)ab棒恰好进入区域Ⅱ,重力加速度为g.求: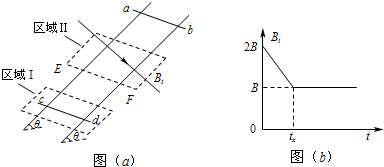 (2011?虹口区二模)如图(a)所示,间距为l、电阻不计的光滑导轨固定在倾角为θ的斜面上.在区域I内有方向垂直于斜面的匀强磁场,磁感应强度恒为B不变;在区域Ⅱ内有垂直于斜面向下的匀强磁场,其磁感应强度Bt的大小随时间t变化的规律如图(b)所示.t=0时刻在轨道上端的金属细棒ab从如图位置由静止开始沿导轨下滑,同时下端的另一金属细棒cd在位于区域I内的导轨上也由静止释放.在ab棒运动到区域Ⅱ的下边界EF之前,cd棒始终静止不动,两棒均与导轨接触良好.
(2011?虹口区二模)如图(a)所示,间距为l、电阻不计的光滑导轨固定在倾角为θ的斜面上.在区域I内有方向垂直于斜面的匀强磁场,磁感应强度恒为B不变;在区域Ⅱ内有垂直于斜面向下的匀强磁场,其磁感应强度Bt的大小随时间t变化的规律如图(b)所示.t=0时刻在轨道上端的金属细棒ab从如图位置由静止开始沿导轨下滑,同时下端的另一金属细棒cd在位于区域I内的导轨上也由静止释放.在ab棒运动到区域Ⅱ的下边界EF之前,cd棒始终静止不动,两棒均与导轨接触良好.