题目内容
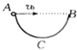 如图所示,AB为半圆环ACB的水平直径,从A点平抛出一小球,小球落到ACB上,
如图所示,AB为半圆环ACB的水平直径,从A点平抛出一小球,小球落到ACB上,(1)若C为ACB弧的中点,直径AB=1.5m,小球下落0.3s后落到ACB上,求:小球抛出的初速度v0 (g取10m/s2 ).
(2)试证明,无论v0取何值,小球都不可能垂直撞击半圆环.
分析:(1)根据时间求出平抛运动的高度,再通过下降的高度结合几何关系求出水平位移,从而求出初速度.
(2)运用假设法进行证明,假设垂直,求出速度与水平方向的夹角,看是否可能.
(2)运用假设法进行证明,假设垂直,求出速度与水平方向的夹角,看是否可能.
解答:解:(1)小球下落高度h=
gt2=
×10×0.09m=0.45m.
小球下落点存在两种可能,根据几何关系,其水平位移可能是x=R±
=0.15m或1.35m.
所以v0=
=0.5m/s或4.5m/s.
(2)设小球垂直击中环,则速度方向必过圆心,设其与水平方向的夹角为θ.
则Rsinθ=
gt2,R(1+cosθ)=v0t
且tanθ=
.可解得θ=0,但这是不可能的.
答:(1)小球平抛的初速度为0.5m/s或4.5m/s.
(2)证明如上.
| 1 |
| 2 |
| 1 |
| 2 |
小球下落点存在两种可能,根据几何关系,其水平位移可能是x=R±
| R2-h2 |
所以v0=
| x |
| t |
(2)设小球垂直击中环,则速度方向必过圆心,设其与水平方向的夹角为θ.
则Rsinθ=
| 1 |
| 2 |
且tanθ=
| gt |
| v0 |
答:(1)小球平抛的初速度为0.5m/s或4.5m/s.
(2)证明如上.
点评:解决本题的关键掌握平抛运动在水平方向和竖直方向上的运动规律,结合几何关系进行求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,AB为半圆环ACB的水平直径,C为环上的最低点,环半径为R.一个小球从A以速度v0水平抛出,不计空气阻力,则下列判断正确的是( )
如图所示,AB为半圆环ACB的水平直径,C为环上的最低点,环半径为R.一个小球从A以速度v0水平抛出,不计空气阻力,则下列判断正确的是( )| A、要使小球掉到环上时的竖直分速度最大,小球应该落在C点 | B、即使v0取值不同,小球掉到环上时的速度方向和水平方向之间的夹角也相同 | C、若v0取值适当,可以使小球垂直撞击半圆环 | D、无论v0取何值,小球都不可能垂直撞击半圆环 |
 如图所示,AB为半圆环ACB的水平直径,C为环上的最低点.一个小球从A点以不同的速度水平抛出,不计空气阻力,下列表述正确的是( )
如图所示,AB为半圆环ACB的水平直径,C为环上的最低点.一个小球从A点以不同的速度水平抛出,不计空气阻力,下列表述正确的是( )
