题目内容
 如图所示,AB为半圆环ACB的水平直径,C为环上的最低点,环半径为R.一个小球从A以速度v0水平抛出,不计空气阻力,则下列判断正确的是( )
如图所示,AB为半圆环ACB的水平直径,C为环上的最低点,环半径为R.一个小球从A以速度v0水平抛出,不计空气阻力,则下列判断正确的是( )| A、要使小球掉到环上时的竖直分速度最大,小球应该落在C点 | B、即使v0取值不同,小球掉到环上时的速度方向和水平方向之间的夹角也相同 | C、若v0取值适当,可以使小球垂直撞击半圆环 | D、无论v0取何值,小球都不可能垂直撞击半圆环 |
分析:小球做平抛运动,可分解为水平方向的匀速直线运动与竖直方向的自由落体运动,应用平抛运动规律分析答题.
解答:解:A、小球在竖直方向做自由落体运动,在竖直方向上:vy2=2gh,vy=
,由此可知,竖直分位移h越大,小球的竖直分速度越大,小球落在C点时的竖直分位移最大,此时的竖直分速度最大,故A正确;
B、小球抛出时的初速度不同,小球落在环上时速度方向与水平方向夹角不同,故B错误;
C、假设小球与BC段垂直撞击,设此时速度与水平方向的夹角为θ,知撞击点与圆心的连线与水平方向的夹角为θ.连接抛出点与撞击点,与水平方向的夹角为β.根据几何关系知,θ=2β.因为平抛运动速度与水平方向夹角的正切值是位移与水平方向夹角正切值的2倍,即tanα=2tanβ.与θ=2β相矛盾.则不可能与半圆弧垂直相撞,故C错误,D正确;
故选:AD.
| 2gh |
B、小球抛出时的初速度不同,小球落在环上时速度方向与水平方向夹角不同,故B错误;
C、假设小球与BC段垂直撞击,设此时速度与水平方向的夹角为θ,知撞击点与圆心的连线与水平方向的夹角为θ.连接抛出点与撞击点,与水平方向的夹角为β.根据几何关系知,θ=2β.因为平抛运动速度与水平方向夹角的正切值是位移与水平方向夹角正切值的2倍,即tanα=2tanβ.与θ=2β相矛盾.则不可能与半圆弧垂直相撞,故C错误,D正确;
故选:AD.
点评:解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,知道平抛运动速度与水平方向的夹角的正切值是位移与水平方向夹角正切值的两倍.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,AB为半圆环ACB的水平直径,C为环上的最低点.一个小球从A点以不同的速度水平抛出,不计空气阻力,下列表述正确的是( )
如图所示,AB为半圆环ACB的水平直径,C为环上的最低点.一个小球从A点以不同的速度水平抛出,不计空气阻力,下列表述正确的是( )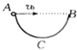 如图所示,AB为半圆环ACB的水平直径,从A点平抛出一小球,小球落到ACB上,
如图所示,AB为半圆环ACB的水平直径,从A点平抛出一小球,小球落到ACB上,
