题目内容
(21分)如图甲所示,在空心三棱柱CDF以外足够大的空间中,充满着磁感应强度为B的匀强磁场。三棱柱的轴线与磁场平行,截面边长为L,三棱柱用绝缘薄板材料制成,其内部有平行于CD侧面的金属板P、Q,两金属板间的距离为d,P板带正电,Q板带负电,Q板中心有一小孔,P板上与小孔正对的位置有一个粒子源S,从S处可以发出初速度为0、带电量为+q、质量为m的粒子,这些粒子与三棱柱侧面碰撞时无能量损失。试求:
(1)为使从S点发出的粒子最终又回到S点,P、Q之间的电压U应满足什么条件?(Q与CD之间距离不计)
(2)粒子从S点出发又回到S点的最短时间是多少?
(3)若磁场是半径为a的圆柱形区域,如图乙所示,圆柱的轴线与三棱柱的轴线重合,且a=( +
+ )L,要使S点发出的粒子最终又回到S点,则P、Q之间的电压不能超过多少?
)L,要使S点发出的粒子最终又回到S点,则P、Q之间的电压不能超过多少?

⑴设粒子到达Q板小孔时的速度为υ,由动能定理得
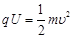 ① (2分)
① (2分)
从小孔发出的粒子在洛伦兹力的作用下做圆周运动,根据牛顿第二定律
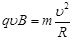 ② (2分)
② (2分)
粒子能回到小孔的条件是: L=2R(2n-1) (n=1,2,3,…) ③ (2分)
由①②③解得
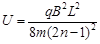 (n=1,2,3,…) ④
(2分)
(n=1,2,3,…) ④
(2分)
⑵粒子在磁场中做圆周运动的周期为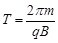 ⑤
⑤
当④式中n=1时,粒子从S出发又回到S时间最短,粒子在磁场中分别以D、F、C为圆心做圆周运动,半径为
R=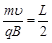 ⑥ (2分)
⑥ (2分)
设粒子从S到小孔所用时间为t1,则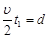 ⑦ (2分)
⑦ (2分)
粒子在磁场中运动的时间为 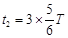 ⑧
(2分)
⑧
(2分)
粒子从S点出发又回到S点的最短时间为 t=2t1+t2 ⑨ (1分)
由以上各式解得
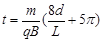 ⑩
(2分)
⑩
(2分)
⑶设D点到磁场边界的最近距离为L1,由已知条件得
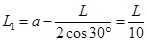 (2分)
(2分)
从S发出的粒子要回到S,就必须在磁场区域内运动,即满足条件
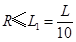
由③④解得 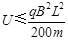 (2分)
(2分)
其他合理解答,同样给分。
【解析】

 阅读快车系列答案
阅读快车系列答案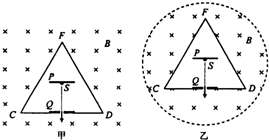 如图甲所示,在空心三棱柱CDF以外足够大的空间中,充满着磁感应强度为B的匀强磁场.三棱柱的轴线与磁场平行,截面边长为L,三棱柱用绝缘薄板材料制成,其内部有平行于CD侧面的金属板P、Q,两金属板间的距离为d,P板带正电,Q板带负电,Q板中心有一小孔,P板上与小孔正对的位置有一个粒子源S,从S处可以发出初速度为0、带电量为+q、质量为m的粒子,这些粒子与三棱柱侧面碰撞时无能量损失.试求:
如图甲所示,在空心三棱柱CDF以外足够大的空间中,充满着磁感应强度为B的匀强磁场.三棱柱的轴线与磁场平行,截面边长为L,三棱柱用绝缘薄板材料制成,其内部有平行于CD侧面的金属板P、Q,两金属板间的距离为d,P板带正电,Q板带负电,Q板中心有一小孔,P板上与小孔正对的位置有一个粒子源S,从S处可以发出初速度为0、带电量为+q、质量为m的粒子,这些粒子与三棱柱侧面碰撞时无能量损失.试求: +
+ )L,要使S点发出的粒子最终又回到S点,则P、Q之间的电压不能超过多少?
)L,要使S点发出的粒子最终又回到S点,则P、Q之间的电压不能超过多少?
