题目内容
在一根细线上套有一个质量为m的光滑小环,将细线的两端固定在如右下图所示的竖直杆上的A、B两点,A、B间距为L,当竖直杆以一定的角速度绕AB轴匀速转动时细线被张紧,小环在水平面内做匀速圆周运动,此时细线的BC段恰沿水平方向且长度为 L.求:
L.求:(1)细线中的拉力大小为多少?
(2)小环做匀速圆周运动的角速度是多少?

【答案】分析:对光滑小环受力分析,受重力和两个拉力;小环做匀速圆周运动,合力提供向心力;根据牛顿第二定律和向心力公式列式求解.
解答:解:设细线中拉力在大小为T,对小球进行受力分析,设∠BAC=θ
在竖直方向上有:Tcosθ=mg
在水平方向上有:T+T sinθ=mω2R
由几何关系知:tanθ=
联立①②③解出:
T=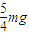
ω=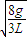
答:(1)细线中的拉力大小为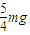 ;
;
(2)小环做匀速圆周运动的角速度是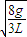 .
.
点评:本题关键是对环受力分析后,根据牛顿第二定律和向心力公式列式求解,不难.
解答:解:设细线中拉力在大小为T,对小球进行受力分析,设∠BAC=θ
在竖直方向上有:Tcosθ=mg
在水平方向上有:T+T sinθ=mω2R
由几何关系知:tanθ=

联立①②③解出:
T=
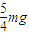
ω=
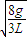
答:(1)细线中的拉力大小为
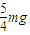 ;
;(2)小环做匀速圆周运动的角速度是
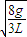 .
.点评:本题关键是对环受力分析后,根据牛顿第二定律和向心力公式列式求解,不难.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2007?黑龙江一模)在一根细线上套有一个质量为m的光滑小环,将细线的两端固定在如右下图所示的竖直杆上的A、B两点,A、B间距为L,当竖直杆以一定的角速度绕AB轴匀速转动时细线被张紧,小环在水平面内做匀速圆周运动,此时细线的BC段恰沿水平方向且长度为
(2007?黑龙江一模)在一根细线上套有一个质量为m的光滑小环,将细线的两端固定在如右下图所示的竖直杆上的A、B两点,A、B间距为L,当竖直杆以一定的角速度绕AB轴匀速转动时细线被张紧,小环在水平面内做匀速圆周运动,此时细线的BC段恰沿水平方向且长度为

