题目内容
19.一个以初速v0水平飞行的子弹,刚好能穿过三个并排置的材料和厚度均相同的木块,则穿过这三个木块所用的时间之比是$(\sqrt{3}-\sqrt{2}):(\sqrt{2}-1):1$,穿过第二个木块时的速度是$\frac{\sqrt{6}}{3}{v}_{0}$.分析 采用逆向思维,结合初速度为零的匀加速直线运动的特殊推论求出穿过三个木块所用的时间之比,根据速度位移公式求出速度之比,从而得出穿过第二个木块的速度大小.
解答 解:子弹刚好穿过第三块木块,采用逆向思维,子弹做初速度为零的匀加速直线运动,因为通过相等位移内所用的时间之比为$1:(\sqrt{2}-1):(\sqrt{3}-\sqrt{2}):$…,
则穿过三个木块所用的时间之比为$(\sqrt{3}-\sqrt{2}):(\sqrt{2}-1):1$.
采用逆向思维,根据$v=\sqrt{2ax}$知,通过相等位移后的速度之比为$1:\sqrt{2}:\sqrt{3}$,则依次穿过三个木块的速度之比为$\sqrt{3}:\sqrt{2}:1$,因为初速度为v0,
则穿过第二个木块的速度为:v=$\frac{\sqrt{6}{v}_{0}}{3}$.
故答案为:$(\sqrt{3}-\sqrt{2}):(\sqrt{2}-1):1$,$\frac{\sqrt{6}{v}_{0}}{3}$.
点评 解决本题的关键掌握匀变速直线运动的运动学公式和推论,并能灵活运用,有时运用推论求解会使问题更加简捷.

练习册系列答案
相关题目
10.宇宙中某双星由质量不等的星体A和B组成,两星在相互之间的万有引力作用下绕两者连线上某一定点C做匀速圆周运动.由天文观察到期运动周期为T,A到C点的距离为r1,A和B的距离为r,已知引力常数为G,由此可求出星体B的质量为( )
| A. | $\frac{4{π}^{2}{r}^{2}{r}_{1}^{\;}}{G{T}^{2}}$ | B. | $\frac{4π{r}_{1}^{2}{r}^{3}}{G{T}^{2}}$ | C. | $\frac{4πr{{\;}^{2}r}_{1}}{G{T}^{2}}$ | D. | $\frac{4π{r}^{2}(r-{r}_{1})}{G{T}^{2}}$ |
7.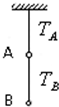 如图所示,两根细线拴着两个静止的质量相同的小球A、B.上、下两根细线中的拉力分别是TA、TB.现在使A、B带同种电荷,再次静止.上、下两根细线拉力分别为TA′、TB′,则( )
如图所示,两根细线拴着两个静止的质量相同的小球A、B.上、下两根细线中的拉力分别是TA、TB.现在使A、B带同种电荷,再次静止.上、下两根细线拉力分别为TA′、TB′,则( )
 如图所示,两根细线拴着两个静止的质量相同的小球A、B.上、下两根细线中的拉力分别是TA、TB.现在使A、B带同种电荷,再次静止.上、下两根细线拉力分别为TA′、TB′,则( )
如图所示,两根细线拴着两个静止的质量相同的小球A、B.上、下两根细线中的拉力分别是TA、TB.现在使A、B带同种电荷,再次静止.上、下两根细线拉力分别为TA′、TB′,则( )| A. | TA′=TA、TB′<TB | B. | TA′=TA、TB′>TB | C. | TA′<TA、TB′>TB | D. | TA′>TA、TB′<TB |
14.已知A、B是第一周期以外的短周期元素,它们可以形成离子化合物AmBn.在此化合物中,所有离子均能形成稀有气体原子的稳定结构.若A的核电荷数为a,则B的核电荷数不可能是( )
| A. | a+8-m-n | B. | a+18-m-n | C. | a+16-m-n | D. | a-m-n |
4.真空中有两个点电荷,它们间的静电力为F,如果保持它们所带的电量不变,将它们之间的距离增大为原来的3倍,它们之间静电力的大小等于( )
| A. | F/9 | B. | F/3 | C. | F | D. | 3F |
11. 如图所示,竖直平面内光滑圆轨道半径R=2m,从最低点A有一质量为m=1kg的小球开始运动,初速度v0方向水平向右,重力加速度g取10m/s2,下列说法不正确的是( )
如图所示,竖直平面内光滑圆轨道半径R=2m,从最低点A有一质量为m=1kg的小球开始运动,初速度v0方向水平向右,重力加速度g取10m/s2,下列说法不正确的是( )
 如图所示,竖直平面内光滑圆轨道半径R=2m,从最低点A有一质量为m=1kg的小球开始运动,初速度v0方向水平向右,重力加速度g取10m/s2,下列说法不正确的是( )
如图所示,竖直平面内光滑圆轨道半径R=2m,从最低点A有一质量为m=1kg的小球开始运动,初速度v0方向水平向右,重力加速度g取10m/s2,下列说法不正确的是( )| A. | 小球能到达最高点B的条件是v0≥4$\sqrt{5}$m/s | |
| B. | 若初速度v0=5m/s,则运动过程中,小球一定不会脱离圆轨道 | |
| C. | 若初速度v0=8m/s,则小球将在离A点2.8m高的位置离开圆轨道 | |
| D. | 若初速度v0=8m/s,则小球离开圆轨道时的速度大小为2$\sqrt{2}$m/s |
8.下列说法中正确的是( )
| A. | 下午2点上课,这里的“下午2点”表示的是时间 | |
| B. | 做加速运动的物体不能被选作参考系 | |
| C. | 研究“歼11”飞机在空中飞行的轨迹时,可以把飞机看成质点 | |
| D. | 考查体操运动员的技术动作时,可以把体操运动员看成质点 |
 如图甲所示,质量为m=50g,长l=10cm的铜棒,用长度也为l的两根轻软导线水平悬吊在竖直向上的匀强磁场中,磁感应强度B=$\frac{1}{3}$T,未通电时,轻线在竖直方向,通入恒定电流后.
如图甲所示,质量为m=50g,长l=10cm的铜棒,用长度也为l的两根轻软导线水平悬吊在竖直向上的匀强磁场中,磁感应强度B=$\frac{1}{3}$T,未通电时,轻线在竖直方向,通入恒定电流后.