题目内容
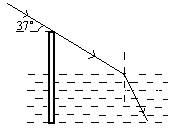
如图所示，一个大游泳池，池底面水平，池水深1.2m，有一竹竿竖直插入池底，浸入水中的部分正好是全长的一半，阳光与水平方向成37°角射入池底，竹竿的影长为2.5m，求水的折射率．分析：先作出光路图．如图所示．根据几何知识求得BD长，得到EF的长度，即可求得入射角i和折射角r的正弦值，由折射定律n=
求出折射率n．
| sini |
| sinr |
解答：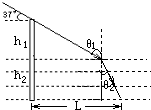
解：作出光路如图所示．
由折射定律有：n=
=
…①
由几何关系有：L=h1cot37°+h2tanθ2 …②
得，tanθ2=
=
=
由②解得：θ2=37°
由①得：n=
答：水的折射率为
．
解：作出光路如图所示．由折射定律有：n=
| sinθ1 |
| sinθ2 |
| sin53° |
| sinθ2 |
由几何关系有：L=h1cot37°+h2tanθ2 …②
得，tanθ2=
| L-h1cot37° |
| h2 |
2.5-1.2×
| ||
| 1.2 |
| 3 |
| 4 |
由②解得：θ2=37°
由①得：n=
| 4 |
| 3 |
答：水的折射率为
| 4 |
| 3 |
点评：解答几何光学问题，首先要正确作出光路图，再根据几何知识求出相关的长度，由折射定律求解n．
练习册系列答案
相关题目
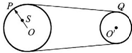如图所示，一个大轮通过皮带拉着小轮转动，皮带和两轮之间无滑动，大轮的半径是小轮的3倍，大轮上的一点s离转动轴的距离是半径的一半，P、S、Q三点的角速度之比=
角射入，池底竿影长2.5m．求水的折射率．
