题目内容
如图所示，一根长为1m的轻杆OA，O端用铰链固定，另一端固定着一个质量为1kg的小球A，轻杆靠在一个质量为2kg、高为0.3m物块上．若物块与地面摩擦不计，则当物块向右运动至杆与水平方向夹角为370时，轻杆的角速度为3rad/s，此时物块的动能为6.25
6.25
J，小球A重力的功率为24
24
W．（g取10m/s2）分析：将物块的速度分解为沿杆子方向和垂直于杆子方向，在垂直于杆子方向上的速度等于B点绕O转动的线速度，根据几何关系求出r，根据v=rω求出物块运动的速度，根据动能的表达式求出物块的动能；根据vA=Lω求出A点线速度，根据功率公式求出小球A重力的功率．
解答：解：当物块以速度v向右运动至杆与水平方向夹角为θ时，B点的线速度等于木块的速度在垂直于杆子方向上的分速度，vB=vsinθ，所以v=
=
=2.5m/s
所以此时物块的动能为；
Mv2=
×2×6.25=6.25J
vA=Lω=3m/s
所以小球A重力的功率为P=mgvAcos37°=24W
故答案为：6.25； 24
| rω |
| sinθ |
| 3×0.5 |
| 0.6 |
所以此时物块的动能为；
| 1 |
| 2 |
| 1 |
| 2 |
vA=Lω=3m/s
所以小球A重力的功率为P=mgvAcos37°=24W
故答案为：6.25； 24
点评：解决本题的关键会根据平行四边形定则对速度进行分解，木块速度在垂直于杆子方向的分速度等于B点转动的线速度、
练习册系列答案
相关题目
如图所示，一根长为L的轻绳一端固定在O′点，另一端系一质量m的小球，小球可视为质点．将轻绳拉至水平并将小球由位置A静止释放，小球运动到最低点时，轻绳刚好被拉断．O′点下方有一以O点为顶点的固定斜面，倾角θ=37°，斜面足够长，且OO′=2L，已知重力加速度为g，忽略空气阻力；求
如图所示，一根长L=1.8m的铁索从楼顶自由下落，则此铁索经过楼顶下距楼顶h=5m的A点，需时间为多少？g=10m/s2．
如图所示，一根长为L=0.2m，质量为m=0.1kg的导线AB，用软导线悬挂在方向水平的磁感应强度为B=1T的磁场中，现要使悬线拉力为零，则：
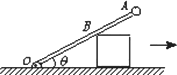
轴在竖直平面内无摩擦转动的细杆AB，两端分别固定质量1kg相等的两个球，已知OB=0.6m。现由水平位置自由释放，求：