题目内容
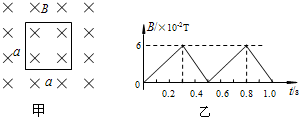 一个边长为a=0.10m的闭合正方形线框,匝数为100,绕制线框的导线单位长度的电阻R0=1.0×10-2Ω?m-1,如图甲所示.线框所在区域存在着匀强磁场,磁场方向垂直线框所在平面向里,磁感应强度随时间变化情况如图乙所示.
一个边长为a=0.10m的闭合正方形线框,匝数为100,绕制线框的导线单位长度的电阻R0=1.0×10-2Ω?m-1,如图甲所示.线框所在区域存在着匀强磁场,磁场方向垂直线框所在平面向里,磁感应强度随时间变化情况如图乙所示.(1)求0~0.3s和0.3s~0.5s 时间内线框中感应电流的大小;
(2)求0~0.3s内导线某横截面通过的电量.
分析:(1)根据法拉第电磁感应定律,求出0~0.3s和0.3s~0.5s 时间内线框中感应电动势的大小,从而根据闭合电路欧姆定律求出感应电流的大小.
(2)根据法拉第电磁感应定律与欧姆定律,结合电量的表达式,即可求解.
(2)根据法拉第电磁感应定律与欧姆定律,结合电量的表达式,即可求解.
解答:解:(1)根据法拉第电磁感应定律E=
,在0~0.3s时间内,感应电动势为:
E1=100×
×0.12V=0.2V,
再根据欧姆定律I=
,则有:I1=
A=0.5A
根据法拉第电磁感应定律E=
,在0.3S~0.5s时间内,感应电动势E2=100×
×0.12V=0.3V,
再根据欧姆定律I=
,则有I2=
A=0.75A
(2)根据法拉第电磁感应定律与欧姆定律,则有Q=
代入数据,解得:Q=
C=0.15C
答:(1)0~0.3s时间内线框中感应电流的大小0.5A;0.3s~0.5s 时间内线框中感应电流的大小0.75A;
(2)0~0.3s内导线某横截面通过的电量0.15C.
| N△B?S |
| △t |
E1=100×
| 6×10-2 |
| 0.3 |
再根据欧姆定律I=
| E |
| R |
| 0.2 |
| 1×10-2×4×0.1×100 |
根据法拉第电磁感应定律E=
| N△B?S |
| △t |
| 6×10-2 |
| 0.2 |
再根据欧姆定律I=
| E |
| R |
| 0.3 |
| 0.4 |
(2)根据法拉第电磁感应定律与欧姆定律,则有Q=
| N△? |
| R |
代入数据,解得:Q=
| 100×6×10-2×0.12 |
| 0.4 |
答:(1)0~0.3s时间内线框中感应电流的大小0.5A;0.3s~0.5s 时间内线框中感应电流的大小0.75A;
(2)0~0.3s内导线某横截面通过的电量0.15C.
点评:本题考查了法拉第电磁感应定律、闭合电路欧姆定律和焦耳定律,难度不大,属于基础题,需加强训练.

练习册系列答案
相关题目
 (2008?内江二模)如图所示,将一个边长为a=0.1m,质量 m=200g,电阻为R=20Ω的正方形金属线框ABCD.以一定的初速度v0=30m/s竖直向上拉出,然后穿过宽度为b=0.4m、磁感应强度为B=20T、方向垂直纸面向外的匀强磁场中.当线框的BC边向上离开磁场边界CH后继续上升了一段高度,然后又自由落下并匀速进入磁场.且线框的BC边向上刚离开磁场时的速度恰好是AD边向上刚进人磁场时速度的一半.在线框运动的整个过程中,线框不发生转动,不计空气的阻力.g=10m/s2.则:
(2008?内江二模)如图所示,将一个边长为a=0.1m,质量 m=200g,电阻为R=20Ω的正方形金属线框ABCD.以一定的初速度v0=30m/s竖直向上拉出,然后穿过宽度为b=0.4m、磁感应强度为B=20T、方向垂直纸面向外的匀强磁场中.当线框的BC边向上离开磁场边界CH后继续上升了一段高度,然后又自由落下并匀速进入磁场.且线框的BC边向上刚离开磁场时的速度恰好是AD边向上刚进人磁场时速度的一半.在线框运动的整个过程中,线框不发生转动,不计空气的阻力.g=10m/s2.则: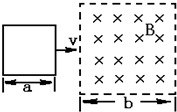 一个边长为a=1m的正方形线圈,总电阻为R=2Ω,当线圈以v=2m/s的速度通过磁感应强度为B=0.5T的匀强磁场区域时,线圈平面总保持与磁场垂直.若磁场的宽度b>1m,如图所示,求:
一个边长为a=1m的正方形线圈,总电阻为R=2Ω,当线圈以v=2m/s的速度通过磁感应强度为B=0.5T的匀强磁场区域时,线圈平面总保持与磁场垂直.若磁场的宽度b>1m,如图所示,求:




 =
=