题目内容
【题目】一质量为m＝2 kg的小球从光滑的斜面上高h＝3.5 m处由静止滑下，斜面底端平滑连接着一个半径R＝1 m的光滑圆环，如图所示，求：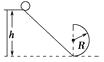
（1）小球滑到圆环顶点时对圆环的压力的大小；
（2）小球至少应从多高处由静止滑下才能越过圆环最高点？（g取10 m/s2）
【答案】
（1）
小球从开始下滑至滑到圆环顶点的过程中，只有重力做功，故可用动能定理求出小球到半圆环最高点时的速度，再由牛顿第二定律求压力．
由机械能综合应用得
mg（h－2R）＝
mv2
小球在圆环最高点时，由牛顿第二定律，得
FN＋mg＝m
联立上述两式，代入数据得
FN＝40 N
由牛顿第三定律知，小球对圆环的压力大小为40 N
（2）
小球能越过圆环最高点的临界条件是在最高点时只有重力提供向心力，即mg＝m①
设小球应从H高处滑下，由机械能综合应用得
mg（H－2R）＝mv′2②
由①②得H＝2.5R＝2.5 m
【解析】（1）小球从开始下滑至滑到圆环顶点的过程中，只有重力做功，故可用动能定理求出小球到半圆环最高点时的速度，再由牛顿第二定律求压力．
由机械能综合应用得
mg（h－2R）＝mv2
小球在圆环最高点时，由牛顿第二定律，得
FN＋mg＝m
联立上述两式，代入数据得
FN＝40 N
由牛顿第三定律知，小球对圆环的压力大小为40 N.（2）小球能越过圆环最高点的临界条件是在最高点时只有重力提供向心力，即mg＝m①
设小球应从H高处滑下，由机械能综合应用得
mg（H－2R）＝mv′2②
由①②得H＝2.5R＝2.5 m.
【考点精析】本题主要考查了机械能综合应用的相关知识点，需要掌握系统初态的总机械能E 1 等于末态的总机械能E 2 ，即E1 =E2；系统减少的总重力势能ΔE P减 等于系统增加的总动能ΔE K增 ，即ΔE P减 =ΔE K增；若系统只有A、
