Question

【题目】如图17所示，半径为R的光滑半圆弧轨道与高为10R的光滑斜轨道放在同一竖直平面内，两轨道之间由一条光滑水平轨道CD相连，水平轨道与斜轨道间有一段圆弧过渡．在水平轨道上，轻质弹簧被a、b两小球挤压，处于静止状态．同时释放两个小球，a球恰好能通过圆弧轨道的最高点A ， b球恰好能到达斜轨道的最高点B.已知a球质量为m1 ， b球质量为m2 ， 重力加速度为g.求：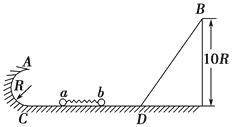

图17
（1）a球离开弹簧时的速度大小va；
（2）b球离开弹簧时的速度大小vb；
（3）释放小球前弹簧的弹性势能Ep.

Answer 1

【答案】
（1）

由a球恰好能到达A点知

m1g＝求出VA=

由机械能综合应用得

m1va2－m1vA2＝m1g·2R

得va＝.

（2）

对于b球由机械能综合应用得：

mbvD2=mbg×10R

得vb=VD=

（3）

由机械能综合应用得

Ep＝m1va2＋m2vb2

得Ep＝7.5mgR.

【解析】（1）
由a球恰好能到达A点知
m1g＝求出VA=
由机械能综合应用得
m1va2－m1vA2＝m1g·2R
得va＝
（2）
对于b球由机械能综合应用得：
mbvD2=mbg×10R
得vb=VD=
（3）
由机械能综合应用得
Ep＝m1va2＋m2vb2
得Ep＝7.5mgR.
【考点精析】解答此题的关键在于理解机械能综合应用的相关知识，掌握系统初态的总机械能E 1 等于末态的总机械能E 2 ，即E1 =E2；系统减少的总重力势能ΔE P减 等于系统增加的总动能ΔE K增 ，即ΔE P减 =ΔE K增；若系统只有A、