题目内容
如图所示,足够长的光滑斜面倾角θ=30°,一个带正电、电量为q的物体停在斜面底端B。现在加上一个沿斜面向上的场强为E的匀强电场,在物体运动到A点时撤销电场,那么:
(1)若已知BA距离x、物体质量m,则物体回到B点时速度大小多少?
(2)若已知物体在斜面上运动的总时间是加电场时间的2倍,则物体的质量m是多少?
(1)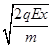 ;(2)
;(2)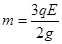 。(3)
。(3)
解析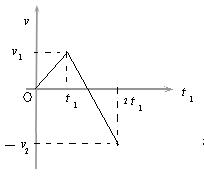
试题分析:
(1)物体由B运动再返回的过程中,重力做功为零,电场力做功为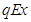 ,根据动能定理得:
,根据动能定理得: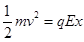 (1)
(1)
解得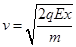 (2);
(2);
由于回到原来位置,即位移为零,则: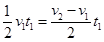 ( 3),
( 3),
得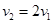 ( 4),
( 4),
(2)设加电场时的时间为t1,该过程末速度大小为v1,返回到原点速度大小为v2,根据题意,整个过程如图所示。那么两过程加速度大小分别为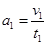 (5 ),
(5 ),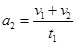 ( 6),
( 6),
可见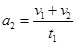 (7 )
(7 )
则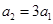 ( 8)。
( 8)。
再对物体在斜面上受力分析:
有电场时受到沿斜面向上的电场力、重力、支持力,根据牛顿第二定律,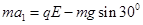 ( 9)
( 9)
没有电场时受到重力、支持力,根据牛顿第二定律,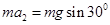 (10 ),
(10 ),
由于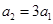 ,代入(9)、(10)可得:
,代入(9)、(10)可得: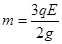 (11)
(11)
考点:本题考查动能定理、匀变速直线位移与时间关系、牛顿第二定律。

练习册系列答案
相关题目


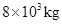 、车长7m的卡车以
、车长7m的卡车以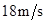 的速度向北匀速行驶,当卡车前端刚驶过停车线AB,该车前方的机动车交通信号灯由绿灯变黄灯。
的速度向北匀速行驶,当卡车前端刚驶过停车线AB,该车前方的机动车交通信号灯由绿灯变黄灯。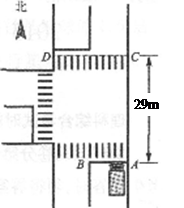
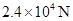 。求卡车的制动距离;
。求卡车的制动距离;