Question

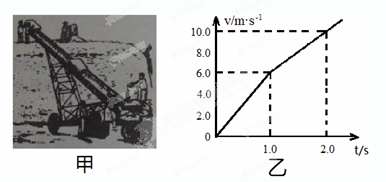
如图所示，一质量为M＝5.0kg的平板车静止在光滑水平地面上，平板车的上表面距离地面高h＝0.8m，其右侧足够远处有一固定障碍物A．另一质量为m＝2.0kg可视为质点的滑块，以v₀＝8m/s的水平初速度从左端滑上平板车，同时对平板车施加一水平向右、大小为5N的恒力F．当滑块运动到平板车的最右端时，两者恰好相对静止．此时车去恒力F．此后当平板车碰到障碍物A时立即停止运动，滑块水平飞离平板车后，恰能无碰撞地沿圆弧切线从B点切入光滑竖直圆弧轨道，并沿轨道下滑．已知滑块与平板车间的动摩擦因数μ＝0.5，圆弧半径为R＝1.0m，圆弧所对的圆心角∠BOD＝θ＝106⁰，g取10m/s²，sin53⁰＝0.8，cos53⁰＝0.6，不计空气阻力，求：

（1）平板车的长度；
（2）障碍物A与圆弧左端B的水平距离；
（3）滑块运动圆弧轨道最低点C时对轨道压力的大小．

Answer 1

（1）4m；（2）1.2m；（3）86N

解析试题分析：
（1）对滑块，由牛顿第二定律得：a₁= =μg=5m/s²       （1分）
对平板车，由牛顿第二定律得： a₂= =3m/s²         （1分）
设经过时间t₁滑块与平板车相对静止，共同速度为v则：v=v₀-a₁t₁=a₂t_1.    
解得：v=3m/s
滑块与平板车在时间t₁内通过的位移分别为：x₁= t₁      （1分）
x₂=t₁       （1分）
则平板车的长度为：L=x₁-x₂=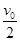t₁=4m          （1分）
（2）设滑块从平板车上滑出后做平抛运动的时间为t₂，则：h=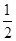gt₂²     （1分）
x_AB=vt₂         （1分）  
解得：x_AB=1.2m       （1分）
（3）对小物块，从离开平板车到C点过程中由动能定理（或机械能守恒定律）得：
mgh+mgR(1-cos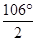)= 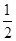mv_c²-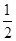mv²           （1分）
在C点由牛顿第二定律得：F_N-mg=m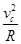     （1分）
解得：F_N="86N"
由牛顿第三定律可知对轨道的压力大小为F _N′=86N     （1分）
考点：本题考查由牛顿第二定律、牛顿第三定律、匀变速运动位移与时间关系、向心力、平抛运动规律。