题目内容
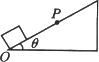
如图所示，物体以200J的初动能从斜面底端向上运动，当它通过斜面上的M点时，其动能减少了160J，机械能减少了64J，最后到达最高点N，则（ ）分析：运用动能定理列出动能的变化和总功的等式，运用除了重力之外的力所做的功量度机械能的变化关系列出等式，两者结合去解决问题．
解答：解：A、由能量守恒得，从出发点到M点，重力势能增加△EP=160J-64J=96J，所以从底端到M点重力做功-96J，故A错误；
B、根据动能定理得从底端到M点其动能减少了160J，所以合外力做功-160J，故B错误
C、运用动能定理分析得出：
物体损失的动能等于物体克服合外力做的功（包括克服重力做功和克服摩擦阻力做功），
损失的动能为：△Ek=mgLsinθ+fL=（mgsinθ+f）L ①
损失的机械能等于克服摩擦阻力做功，△E=fL ②
所以由①②得从M点到N点动能减少了40J，机械能减少了16J，即重力势能增加24J，所以从M点到N点重力做功-24J，故C错误．
D、物体以200J的初动能从斜面底端向上运动，当它通过斜面上的M点时，其动能减少了160J，所以物体在M点动能是40J，所以从M点到N点减小40J，所以合外力做功-40J，故D正确．
故选D．
B、根据动能定理得从底端到M点其动能减少了160J，所以合外力做功-160J，故B错误
C、运用动能定理分析得出：
物体损失的动能等于物体克服合外力做的功（包括克服重力做功和克服摩擦阻力做功），
损失的动能为：△Ek=mgLsinθ+fL=（mgsinθ+f）L ①
损失的机械能等于克服摩擦阻力做功，△E=fL ②
所以由①②得从M点到N点动能减少了40J，机械能减少了16J，即重力势能增加24J，所以从M点到N点重力做功-24J，故C错误．
D、物体以200J的初动能从斜面底端向上运动，当它通过斜面上的M点时，其动能减少了160J，所以物体在M点动能是40J，所以从M点到N点减小40J，所以合外力做功-40J，故D正确．
故选D．
点评：解题的关键在于能够熟悉各种形式的能量转化通过什么力做功来量度，并能加以运用列出等式关系．
练习册系列答案
相关题目
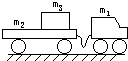在光滑水平面上，有一质量m1=20kg的小车，通过一根几乎不可伸长的轻绳与另一个质量为m2=25kg的拖车相连接．一质量m3=15kg的物体放在拖车的平板上．物体与平板间的动摩擦因数为μ=0.20．开始时，拖车静止，绳未拉紧，如图所示，小车以v0=3m/s的速度向前运动．求：
（填“最高点”或“最低点”）开始计时。
；已知
，玻璃球在1分钟内完成20次全振动，则管径
。