题目内容
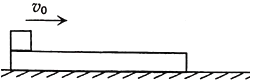
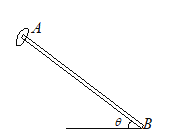
【题目】如图所示,遥控赛车比赛中一个规定项目是“飞跃壕沟”,比赛要求:赛车从起点出发,沿水平直轨道运动,在B点飞出后越过“壕沟”,落在平台EF段。已知赛车的额定功率P=10.0W,赛车的质量m=1.0kg,在水平直轨道上受到的阻力f=2.0N,AB段长L=10.0m,BE的高度差h=1.25m,BE的水平距离x=1.5m。若赛车车长不计,空气阻力不计,g取10m/s2。
(1)若赛车在水平直轨道上能达到最大速度,求最大速度vm的大小;
(2)要越过壕沟,求赛车在B点最小速度v的大小;
(3)若在比赛中赛车通过A点时速度vA=1m/s,且赛车达到额定功率。要使赛车完成比赛,求赛车在AB段通电的最短时间t。

【答案】(1)5 m/s (2) 3.0m/s (3)2.4s
【解析】
(1)赛车在水平轨道上达到最大速度时,设其牵引力为F,根据牛顿第二定律有
F-f=0
又因为 P=Fvm1
所以![]() m/s
m/s
(2)赛车通过B点在空中做平抛运动,设赛车能越过壕沟的最小速度为v,在空中运动时间为t1,则有![]()
且x=vt1
所以v=3.0m/s
(3)若赛车恰好能越过壕沟,且赛车通电时间最短,在赛车从A点运动到B点的过程中根据动能定理有:![]()
带入数据解得:t=2.4s

练习册系列答案
相关题目