题目内容
【题目】如图1所示,在光滑的水平面上,有一质量m=1kg、足够长的U型金属导轨abcd,间距L=1m。一电阻值![]() 的细导体棒MN垂直于导轨放置,并被固定在水平面上的两立柱挡住,导体棒MN与导轨间的动摩擦因数
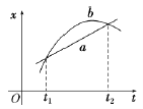
的细导体棒MN垂直于导轨放置,并被固定在水平面上的两立柱挡住,导体棒MN与导轨间的动摩擦因数![]() ,在M、N两端接有一理想电压表(图中未画出)。在U型导轨bc边右侧存在垂直向下、大小B=0.5T的匀强磁场(从上向下看);在两立柱左侧U型金属导轨内存在方向水平向左,大小为B的匀强磁场。以U型导轨bc边初始位置为原点O建立坐标x轴。t=0时,U型导轨bc边在外力F作用下从静止开始运动时,测得电压与时间的关系如图2所示。经过时间t1=2s,撤去外力F,直至U型导轨静止。已知2s内外力F做功W=14.4J。不计其他电阻,导体棒MN始终与导轨垂直,忽略导体棒MN的重力。求:
,在M、N两端接有一理想电压表(图中未画出)。在U型导轨bc边右侧存在垂直向下、大小B=0.5T的匀强磁场(从上向下看);在两立柱左侧U型金属导轨内存在方向水平向左,大小为B的匀强磁场。以U型导轨bc边初始位置为原点O建立坐标x轴。t=0时,U型导轨bc边在外力F作用下从静止开始运动时,测得电压与时间的关系如图2所示。经过时间t1=2s,撤去外力F,直至U型导轨静止。已知2s内外力F做功W=14.4J。不计其他电阻,导体棒MN始终与导轨垂直,忽略导体棒MN的重力。求:
(1)在2s内外力F随时间t的变化规律;
(2)在整个运动过程中,电路消耗的焦耳热Q;
(3)在整个运动过程中,U型导轨bc边速度与位置坐标x的函数关系式。

【答案】(1)![]() ;(2)12J;(3)
;(2)12J;(3)![]() (0≤x≤4m);
(0≤x≤4m);![]()
![]() ;v=0(
;v=0(![]() )
)
【解析】
(1)根据法拉第电磁感应定律可知:
![]()
得到:
![]()
根据速度与时间关系可知:
![]()
对U型金属导轨根据牛顿第二定律有:
![]()
带入数据整理可以得到:
![]()
(2)由功能关系,有
![]()
由于忽略导体棒MN的重力,所以摩擦力为:
![]()
则可以得到:
![]()
则整理可以得到:
![]()
得到:
Q=12J
(3)设从开始运动到撤去外力F这段时间为![]() ,这段时间内做匀加速运动;
,这段时间内做匀加速运动;
①![]() 时,根据位移与速度关系可知:
时,根据位移与速度关系可知:
![]()
![]() 时根据匀变速运动规律可知该时刻速度和位移为:
时根据匀变速运动规律可知该时刻速度和位移为:
![]()
![]()
②![]() 时,物体做变速运动,由动量定理得到:
时,物体做变速运动,由动量定理得到:
![]()
整理可以得到:
![]()
当![]() 时:
时:
![]()
综合上述,故bc边速度与位置坐标x的函数关系如下:
![]() (0≤x≤4m)
(0≤x≤4m)
![]()
![]()
![]() (
(![]() )
)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目