题目内容
10.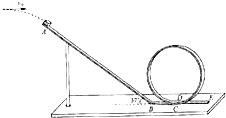 为了研究过山车的原理,物理小组提出了下列的设想:取一个与水平方向夹角为37°、长为L=2.0m的粗糙的倾斜轨道AB,通过水平轨道BC与竖直圆轨道相连,出口为水平轨道DE,整个轨道除AB段以外都是光滑的.其中AB与BC轨道以微小圆弧相接,如图所示.一个小物块以初速度v0=4.0m/s,从某一高处水平抛出,到A点时速度方向恰沿AB方向,并沿倾斜轨道滑下.已知物块与倾斜轨道的动摩擦因数μ=0.50(g取10m/s2,sin37°=0.60,cos37°=0.80)求:
为了研究过山车的原理,物理小组提出了下列的设想:取一个与水平方向夹角为37°、长为L=2.0m的粗糙的倾斜轨道AB,通过水平轨道BC与竖直圆轨道相连,出口为水平轨道DE,整个轨道除AB段以外都是光滑的.其中AB与BC轨道以微小圆弧相接,如图所示.一个小物块以初速度v0=4.0m/s,从某一高处水平抛出,到A点时速度方向恰沿AB方向,并沿倾斜轨道滑下.已知物块与倾斜轨道的动摩擦因数μ=0.50(g取10m/s2,sin37°=0.60,cos37°=0.80)求:(1)小物块的抛出点和A点的高度差;
(2)要使小物体不离开轨道,并从水平轨道DE滑出,求竖直圆弧轨道的半径应该满足什么条件
(3)a.为了让小物块不离开轨道,并且能滑回倾斜轨道AB,求竖直圆弧轨道的半径应该满足什么条件;
b.按照“a”的要求,小物块进入轨道后可以有多少次通过圆轨道上距水平轨道高为0.01m的某一点.
分析 (1)通过平抛运动的规律求出小物块到达A处时下落的高度,根据牛顿第二定律求出小物块在最高点的最小速度,通过全过程运用动能定理求出竖直圆轨道的半径应该满足的条件.
(2)a.为了让物块不离开轨道,并且能够滑回倾斜轨道AB,则物块上升的高度须小于或等于R0′,则根据动能定理求出竖直轨道的半径应该满足的条件.
b.根据动能定理求出再次进入圆轨道到达的高度和第一次冲上圆轨道的高度关系,得出上升n次后高度的通项式,从而得出小物块进入轨道后可以有多少次通过圆轨道上距水平轨道高为0.O1m的某一点.
解答 解:(1)物体做平抛运动,到达A处时,令下落的高度为h,水平分速度为vx,竖直分速度为vy,则由平抛运动的规律可知:
tan37°=$\frac{{v}_{y}}{{v}_{x}}$,vx=v0,vy2=2gh
物体落在斜面上后,受到斜面的摩擦力为:f=μN=μmgcos37°.
设物块进入圆轨道到最高点时有最小速度v1,此时物块受到的重力恰好提供向心力了,令轨道的轨道半径为R0.由牛顿第二定律知:
mg=m$\frac{{v}_{1}^{2}}{{R}_{0}}$
物块从抛出到圆轨道最高点的过程中,由动能定理知:
mg(h+Lsin37°)-μmgcos37°•L-2mgR0=$\frac{1}{2}$mv12-$\frac{1}{2}$mv02
联立上面各式解得:R0=0.66m.
若物块从水平轨道DE滑出,则竖直圆轨道的半径R1≤0.66m.
(2)a.为了让物块不离开轨道,并且能够滑回倾斜轨道AB,则物块上升的高度须小于或等于R0′,则根据动能定理得:
mg(h+Lsin37°)-μmgcos37°•L-mgR0′=0-$\frac{1}{2}$mv02
代入数据得:R0′=1.65m.
若物块能够滑回倾斜轨道AB,则R2≥1.65m.
b.若物块冲上圆轨道H1=1.65m高度时速度变为0,然后又返回倾斜轨道h1高处再滑下,然后再次进入圆轨道达到的高度为H2,则有:
mgH1=mgh1+μmgh1•$\frac{4}{3}$mgH2=mgh1-μmgh1•$\frac{4}{3}$
解得:H2=$\frac{1-\frac{4}{3}μ}{4}$H1=$\frac{1}{5}$H1.
之后物块在竖直圆轨道和倾斜轨道之间往复运动,同理,n次上升的高度:
Hn=($\frac{1}{5}$)n-1H1(n>0)为一等比数列.
可见当n=5时,上升的最大高度小于0.01m,则物块共有8次通过圆轨道上距水平轨道高为0.01m的某一点.
答:(1)竖直圆轨道的半径应该满足R1≤0.66m.
(2)a.竖直圆轨道的半径应该满足R2≥1.65m.
b.小物块进入轨道后可以有8次通过圆轨道上距水平轨道高为0.O1m的某一点.
点评 本题综合考查了动能定理和牛顿第二定律,涉及到平抛运动,直线运动和圆周运动,综合性较强,对学生的能力要求较高,需加强这方面的训练.

 阅读快车系列答案
阅读快车系列答案| A. | U增大,E增大 | B. | U增大,E不变 | C. | U不变,E减小 | D. | U减小,E减小 |
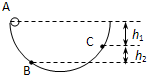 如图所示,一物体从圆弧形轨道的A点无初速滑下,物体与圆弧轨道间的动摩擦因数为μ,由于摩擦力的作用物体沿轨道到达C点时的速度为零,C点比A点下降了h1,物体又由C点沿轨道滑至B点,速度再次为零,B比C下降了h2,则h1与h2比较有( )
如图所示,一物体从圆弧形轨道的A点无初速滑下,物体与圆弧轨道间的动摩擦因数为μ,由于摩擦力的作用物体沿轨道到达C点时的速度为零,C点比A点下降了h1,物体又由C点沿轨道滑至B点,速度再次为零,B比C下降了h2,则h1与h2比较有( )| A. | h1>h2 | B. | h1<h2 | C. | h1=h2 | D. | 无法确定 |
| A. | 人受到的摩擦力的方向是沿杆向下的 | |
| B. | 人受到的摩擦力的方向是沿杆向上的 | |
| C. | 人握旗杆用力越大,人受的摩擦力也越大 | |
| D. | 人握旗杆用力越大,并不会使人受的摩擦力增大 |

 图中工人在推动一台割草机,施加的力大小为100N,方向与水平地面成30°斜向下.g=10m/s2
图中工人在推动一台割草机,施加的力大小为100N,方向与水平地面成30°斜向下.g=10m/s2 如图所示,固定的光滑半球形容器半径为R,其最底点C与球心O的连线垂直水平面,质量为m的小球在A点以某个初速沿着半球容器切线下滑,恰能滑到容器边沿B处.在这过程中重力做功为-0.6mgR;弹力做功为0;球在A处的速度大小为$\sqrt{1.2gR}$.
如图所示,固定的光滑半球形容器半径为R,其最底点C与球心O的连线垂直水平面,质量为m的小球在A点以某个初速沿着半球容器切线下滑,恰能滑到容器边沿B处.在这过程中重力做功为-0.6mgR;弹力做功为0;球在A处的速度大小为$\sqrt{1.2gR}$.