题目内容
一辆质量为m的汽车，从静止开始以额定功率P在平直公路上做直线运动，运动中受到恒定阻力f的作用，经过时间t车速达到最大值，则在该段时间t内汽车运动的路程为 ．
分析：汽车行驶速度达到最大时牵引力与受到的阻力Ff大小相等，根据公式P=fv求得最大速度；再由全程中的动能定理求得经过的总路程．
解答：解：当汽车的阻力等于牵引力时速度达到最大
由P=FV=fV得
V=
在整个过程中有动能定理可得
Pt-fx=
mv2
解得
x=
-
故答案为
-
由P=FV=fV得
V=
| P |
| f |
在整个过程中有动能定理可得
Pt-fx=
| 1 |
| 2 |
解得
x=
| Pt |
| f |
| mP2 |
| 2f2 |
故答案为
| Pt |
| f |
| mP2 |
| 2f2 |
点评：本题为机车启动问题，注意当牵引力等于阻力时速度达到最大值，该题难度适中
练习册系列答案
全能测控期末小状元系列答案
相关题目
如图所示，一辆质量为m的汽车，以恒定的输出功率P在倾角为θ的斜坡上沿坡匀速向上行驶，汽车受到的摩擦阻力恒为汽车重力的K倍（忽略空气阻力），则汽车的牵引力大小为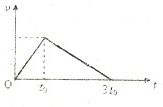
一辆质量为m的汽车在发动机牵引力F的作用下，沿水平方向运动．在t0时刻关闭发动机，其运动的v-t图象如图所示．已知汽车行驶过程中所受的阻力是汽车重量的k倍，则（ ）
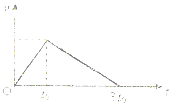一辆质量为m的汽车在发动机牵引力F的作用下，沿水平方向运动．在t0时刻关闭发动机，其运动的v-t图象如图所示．已知汽车行驶过程中所受的阻力是汽车重量的k倍，则（ ）