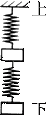题目内容
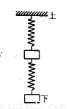
Sl和S2表示劲度系数分别为k1和k2的两根弹簧。k1>k2,a和b表示质量分别为ma和mb的两个物块,ma>mb,将弹簧与物块按图所示方式悬挂起来。现要求两根弹簧的总长度最大,则应使 ( )
A.Sl在上,a在上 B.Sl在上,b在上
C.S2在上,b在上 D.S2在上,a在上
【答案】
C
【解析】
试题分析:当系统平衡时,上边的弹簧所受的弹力F上=(ma+mb)g,与a,b的位置无关。根据胡克定律F=kx,欲使下边弹簧伸长量最大,其所受弹力应最大。所以应该a下b上。对下面的弹簧则mag=k下x下,所以x下=mag/k下。对上边弹簧,则(ma+mb)g=k上x上,所以x上=(ma+mb)g/k上。由于k1>k2,
欲使x下+x上最大,显然应取k上=k2,k下=k1即S2上,S1下。所以本题选择C。
考点:共点力的平衡、胡克定律

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
如图,Sl和S2表示劲度系数分别为kl和k2的两根弹簧,k1 >k2;a和b表示质量分别为m1和m2 的两个小物块,m1>m2.将弹簧与物块按图示方式悬挂起来。现要求两根弹簧的总长度最大,则应使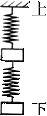
| A.S1在上,a在上 |
| B.S1在上,b在上 |
| C.S2在上,a在上 |
| D.S2在上,b在上 |
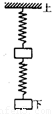
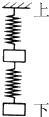 Sl和S2表示劲度系数分别为kl和k2的两根弹簧,k1>k2;a和b表示质量分别为ma和mb 的两个小物块,ma>mb.将弹簧与物块按图示方式悬挂起来.若当S1、S2、a、b适当放置时,两弹簧的总长度最大,在图中标出S1、S2、a、b并求这时两根弹簧的形变量之和(重力加速度为g).
Sl和S2表示劲度系数分别为kl和k2的两根弹簧,k1>k2;a和b表示质量分别为ma和mb 的两个小物块,ma>mb.将弹簧与物块按图示方式悬挂起来.若当S1、S2、a、b适当放置时,两弹簧的总长度最大,在图中标出S1、S2、a、b并求这时两根弹簧的形变量之和(重力加速度为g).